Not sure about utility function being $\min$ and it being a case of perfect substitutes...
In general, I would say there are a few different types of utility functions but if you know more or less the theory and can imagine various functions' graphs, then (as mentioned in the comment) you will be fine.
So I think we should start with a Cobb-Douglas preferences which can be represented by utility function of the form: $$u(x_1,x_2) = x_1^ax_2^b \:\:\: \textrm{for} \:\:\:a>0 \:\: \textrm{and} \:\: b>0$$

Then you have a perfect-substitute preferences which can be represented by utility function of the form: $$u(x_1,x_2) = ax_1 + bx_2 \:\:\: \textrm{for} \:\:\:a>0 \:\: \textrm{and} \:\: b>0$$

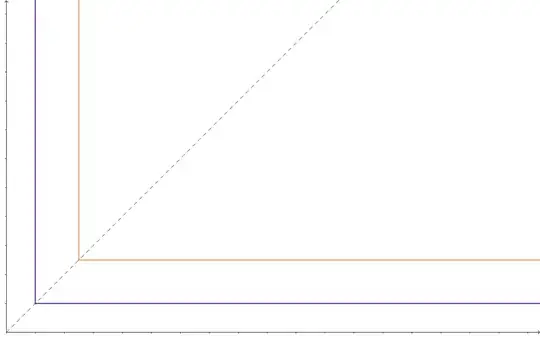
You can also have a perfect-complement preferences which can be represented by utility function of the form: $$u(x_1,x_2) = \min\{ax_1,bx_2\} \:\:\: \textrm{for} \:\:\:a>0 \:\: \textrm{and} \:\: b>0$$
Finally, you can have a quasi-linear preferences which can be represented by utility function of the form: $$u(x_1,x_2) = f(x_1) +x_2 \:\:\: \textrm{where f is increasing and concave}$$

In all of the above graphs I assumed $a=b=1$ for simplicity. In the last case the concave function was a square root.
Your example is (more or less):
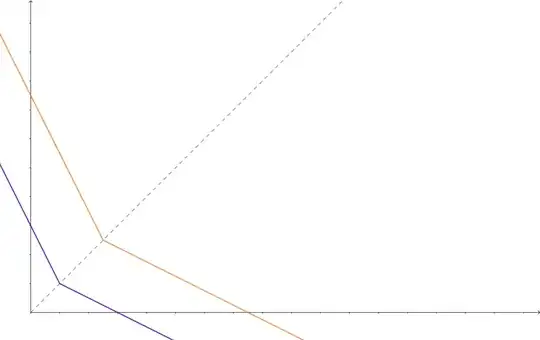
You can now try and argue what kind of preferences these are.
If you are interested in consumer theory, you should find some proper course book or other materials - there's plenty of it on the Internet - just google it.
The last piece of advice I can give you - try to draw as many graphs as you can think of and then try to find a story that the graph is explaining. Or the other way round. I remember my professors trying to "play" with us by giving us different kinds of utility functions - when you drew them, they looked "strange" but when you actually thought about them - they did have some story to tell.
EDIT.
There is also a special case in a way - monotonic transformation is a real-valued function $f: \mathbb{R} \to \mathbb{R}$ which basically transforms numbers into numbers in a way that preserves the order of the numbers, that is, for every two numbers $p$ and $k$ it hods that $p>k \implies f(p)>f(k) $. This means that if a function $f$ is a monotonic transformation of utility $u( \cdot )$, then $f(u(\cdot))$ also represents the consumer’s preferences. $$(x_1,x_2) \succeq (y_1,y_2) \iff f(u(x_1,x_2)) > f (u(y_1,y_2))$$
All this means is that you need to be careful for a case of utility function like: $\ln{x_1} + \ln{x_2}$ which is just a natural logarithm of Cobb-Douglas preferences $x_1x_2$ with $a=b=1$.




