12

This paper gives a proof that in a game with doors and pressure plates, it is PSPACE-hard to determine whether or not the (player's) avatar can reach a given location. This is proven by a reduction from TQBF, and the length of the resulting solutions depends exponentially on the number of universal quantifiers in the formula.

Is there a reduction from an NPSPACE machine to such a game for which the length of the game's solutions are polynomially related to the length of the machine's accepting paths?

Jeffε
  • 23,129
  • 10
  • 96
  • 163
  • 1
    brief sketch of a more formal defn of "game with doors and pressure plates" [alas, not really given in the paper in one place]. the generalized game is an infinite 2d map that can be represented as a graph (of arbitrary size) of connecting spaces/regions. nodes of the graph are spaces/regions (equiv, cells/tunnels etc), edges are doors between them. the pressure plates are switches contained in the spaces. a switch controls a door opening. doors start out in an arbitrary state, maybe some open, some closed. (etc.) ... however, it does appear that the author is only considering planar graphs. – vzn Aug 21 '13 at 17:07
  • furthermore, the question seems to be close to, or nearly equivalent, to the question of whether the length of the minimal path of a solution (counted in edges) through the graph is polynomially or exponentially related to the size of the graph/switches... this in turn seems to be closely related to the question of how many cycles in the path are necessary or if they are not... – vzn Aug 22 '13 at 01:01

3 Answers3

2

Perhaps you can easily simulate a LBA; the idea is the following:

  • for every cell of the LBA tape add a cell gadget $G_i$ that can be entered only from the bottom and leaved only from the top;

  • the gadget has an entrance door $C_i$ which simulates the head position (only one $C_i$ is opened at every step);

  • then there are two bit doors $Z_i$ and $O_i$; $Z_i$ is opened if the cell contains a zero, $O_i$ is opened if there cell contains a one;

  • both bit doors lead to a similar control structure which is made by several one-way corridors; a corridor corresponds to a state of the LBA, and the door $q_i$ of the $i$-th corridor is opened if and only if the current state of the LBA is $q_i$;

  • according to the (possibly non-deterministic) transition table of the LBA, a traversal of the (opened) corridor changes the current state of the LBA and the configuration of the bit-doors, closes door $C_i$ and opens $C_{i+1}$ or $C_{i-1}$.

A cell gadget is sketched in the figure below.

enter image description here

Non-deterministic choices can be realized splitting the corridors in the control structures into two or more sub-corridors as shown in the figure below.

enter image description here

Note: if a plate can only open/close a single door, then you can add an auxiliary structure with (long) one way corridors that (de)activates the distinct state doors of each cell.

Marzio De Biasi
  • 22,915
  • 2
  • 58
  • 127
  • If a door can only be opened by a single plate and can only be closed by a single plate, then you can use crossover gadgets (which I could describe) to let the corridors lead only to the entrance of the desired cell (which removes the need for the C1 doors), implement Z1 and O1 with lots of different doors, each of which has a closing plate immediately after it, and implementing the q0,...,q4 doors as lots of mini-corridors with two doors each followed by a plate that closes one of those two doors and a plate that closes one of the open pair of doors on the other [cell-value]'s qi. $;;;$ –  Aug 20 '13 at 17:24
  • Independently of the suggestions in my previous comment, if the LBA is non-deterministic then $\hspace{.2 in}$ the one-way corridors would need sub-corridors, to indicate the non-deterministic choice. $\hspace{.6 in}$ –  Aug 20 '13 at 17:29
  • ?? isnt LBA recognition = (N)PSPACE? seems it would be more helpful if the answer was phrased in terms of a complexity class. – vzn Aug 20 '13 at 21:38
  • @RickyDemer: ok, I added an example of a non-deterministic choice. Are you using Viglietta's metatheorems to prove the complexity of some games? – Marzio De Biasi Aug 20 '13 at 22:57
  • I was reading his metatheorems, and realized that this is one thing they don't address. $\hspace{.69 in}$ –  Aug 21 '13 at 00:32
2

Another quick way to prove the Metatheorem 2c (PSPACE-hardness when the doors are controlled by two plates) is to use the Nondeterministic Constraint Logic framework (R.A. Hearn and E.D. Demaine, The Nondeterministic Constraint Logic Model of Computation: Reductions and Applications).

In this case it is sufficient to use an horizontal series of vertical corridors-pairs. The state of each pair of corridors represents the direction (inward/outward) of an edge in the original constraint graph. It is sufficient to simulate the AND gadget and OR gadget, like sketched in the figure below.

enter image description here

Marzio De Biasi
  • 22,915
  • 2
  • 58
  • 127
-5

this type of research of relating video games to computational complexity is quite intriguing but it is also quite new, generally less than a decade old. I will argue here there is subtlety that is sometimes being missed in the current analyses [have not seen/noticed this pointed out in the cited paper or other papers so far] and that impedes answering the stated question definitely.

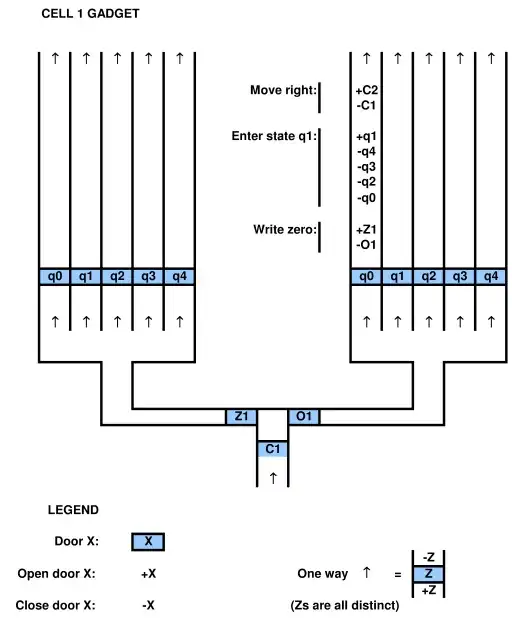
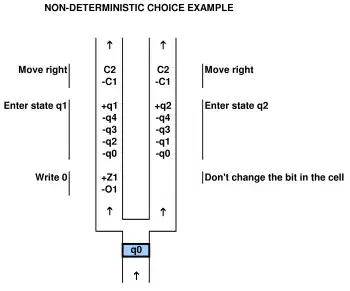
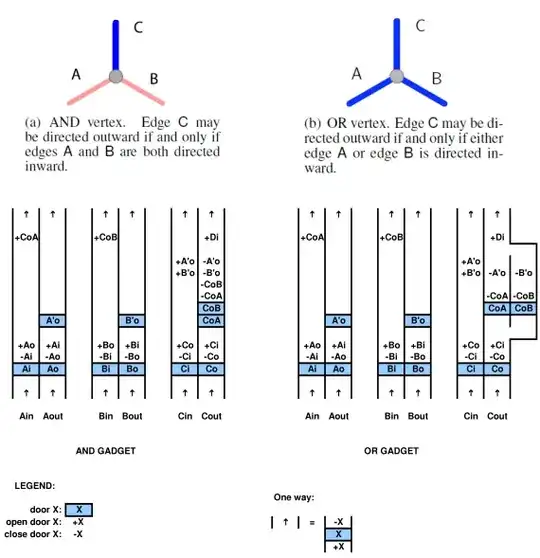
to prove a relation to a computational system, one must be able to map the computational system onto the game and vice versa. for example in the above cited paper by Viglietta there is a concept that pressure plates and doors (ie the pressure plates control doors) can be "like" QBFs. this analogy is certainly viable as they have mapped it out. one can use a QBF to solve a game with pressure plates and doors.

however, here is the subtlety. in a given game, the layouts of the game are basically fixed. in video game design the concept of different layouts is called "layout design" and is not a "given" of all games. for example in the groundbreaking game Doom, the level design tools were open-sourced ie made available to players to use. in other words arbitrary level design can be regarded as part of the game. but in other games considered in papers, the video games as originally built have fixed levels. the papers are sometimes not explicitly taking this into account.

therefore there is a strong argument to be made that in most games without level design, or random layouts, levels are fixed, and this has a big impact on the actual complexity of solving the "game". ie, what exactly is the "game"? does it include random layouts, and/or level design possibility? is level design part of the computational mapping? these issues are glossed over somewhat in current papers.

taken to the opposite extreme of the papers, one could argue that all real video game implementations are solvable by FSMs because they have finite memory!

for there to be real computational mappings, basically one must generalize the game to involve

  • levels with arbitrary size! so that this can be mapped to TMs with arbitrary/unlimited size "input" tapes.
  • level design that allows creation of these levels.

a slightly similar mapping issue arises in CA/Cellular Automata research where there are ideas about using infinite periodic patterns on the CAs as "starting patterns" to prove TM equivalence/completeness.

so in general your question is not strictly defined until you clarify better (ie more formally/mathematically define) what you mean by "in a game with doors and pressure plates" and in a way that even the paper does not apparently strictly define, esp wrt to ideas about level design, unlimited size levels, etcetera. but notice that the "games" defined with these features then have been abstracted away from the actual/real video games in a very significant way.

so in short I think this is interesting/worthwhile research, even though starting out as somewhat informal, and deserves further advancement, but to some degree its formalization must be made more strict esp in basic definitions if it is to advance further. it must make a more strict/formal/transparent distinction between the implementations and the abstractions.

vzn
  • 11,014
  • 2
  • 31
  • 64
  • for example here is a paper on Battleship as NP complete, but it better/formally states/describes the NP complete generalization of the limited-size game. Battleships as a decision problem by Sevenster, sec2. – vzn Aug 20 '13 at 16:57
  • another example of subtleties in generalizing/abstracting the problem, generalization of the 15-puzzle geometry can affect its NP completeness. note a square vs rectangular grid can affect results. – vzn Aug 20 '13 at 17:09
  • 7
    While this is an issue, I think your claim that this is glossed over in the literature is badly overstated. And given the existence of papers like Fraenkel et al FOCS 1978 on the complexity of checkers, Even and Tarjan JACM 1976 on Hex, and Robertson and Munro Util. Math. 1978 on Instant Insanity, your claim that this is a brand new area is also badly overstated. – David Eppstein Aug 20 '13 at 18:55
  • obviously games in general studied from a TCS view are not new, its video games that are, as the text is careful to state. – vzn Aug 20 '13 at 20:35
  • 1
    Mahjong solitaire: 1994. Minesweeper: 2000. Tetris: 2002. Do these not count as video games, or do you use a long decade? – Peter Shor Aug 20 '13 at 23:59
  • Also, Video Checkers for Atari was released in about 1980. – David Eppstein Aug 21 '13 at 03:41
  • guys, great, yeah! [arcade] video games have been around for decades starting with pong ~1970! & some date to the 1950s! the TCS study of video games, esp arcade games as in the Viglietta ref is relatively recent and not even published much in journals yet! shor, the mahjong ref in the paper is interesting/early but video games are not mentioned at all in the title or abstract! also minesweeper ref on wikipedia states it dates to 1960s/70s mainframes, yet your early TCS ref is 2000. the point is, as stated, the scientific/TCS study is "relatively recent" ie roughly within a decade... – vzn Aug 21 '13 at 16:21
  • also, the ideas of mapping gameplay to computational complexity classes, which requires, in a sense as pointed out above, "infinitizing" the finite game, that seems to be the more recent theoretical invention (around a decade old).... but yes its like a variation on working with large chess squares, an old idea.... but the point is with video games & their inherent complexity, the infinitizing step nec requires more attn/definition/care than with a simple case like a chess square.... – vzn Aug 21 '13 at 16:30
  • "Work in this field is often distinguished by its emphasis on mathematical technique and rigor." – vzn Aug 21 '13 at 16:33