35

I am interested in the natural generalization of the famous 15-puzzle, where you have to slide blocks until you have sorted all given numbers (usally there is a gap of 1 block).

Now the generalization would be to extend the size of the puzzle from 15 to $p \times q$, where one field is free. I have created a small illustration (the dashed arrows show permitted moves and the lower configuration shows the solved puzzle):

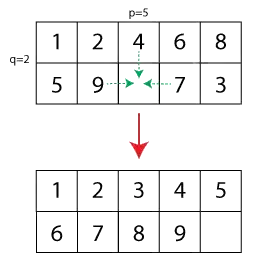
enter image description here

Given an initial configuration of a puzzle, I ask myself the following question:

Decision question: Given a puzzle of size $p \times q$, and a number $k \in \mathbb{N}$. Is there a sequence of $k$ or less allowed moves that transform the puzzle into the solved configuration?

I already did some investigation and found the article "The $(n^2−1)$-puzzle and related relocation problems" from 1990, which shows that deciding my question for $p=q$ is NP-Complete and therefore that deciding my question is NP-Complete (as the general algorithm could also decide the question for symmetric fields).

The question that remains open is if the decision problem is also NP-Complete for fixed $q>1$. I am particularily interested in the special cases $q=2,3$. It also remains open if allowing more free spaces than one field makes the decision problem harder or easier.

All the articles I could find sadly omit the asymmetric case, thus I think there might be no known results about this. As the proof in the article is quite complicated and doesn't translate at all for fixed height, I rather hope that someone might come up with a different reduction/article that answers some of the questions.

Other related articles (to be extended):

Gilles 'SO- stop being evil'
  • 2,667
  • 1
  • 27
  • 35
Listing
  • 607
  • 5
  • 13
  • I agree with Shaull – Marzio De Biasi Feb 21 '13 at 13:08
  • @Vor Is there some mechanism that allows me to migrate it myself, or should I delete and repost the question? –  Feb 21 '13 at 13:09
  • 2
    @Listing: no you cannot do it yourself, moderators can move it (perhaps they will notice these comments, and if they agree they will move it). – Marzio De Biasi Feb 21 '13 at 13:14
  • Do you know http://red.cs.nott.ac.uk/~gxk/papers/icga2008_preprint.pdf ? – frafl Feb 21 '13 at 14:25
  • 1
    @frafl yes I read that but didn't mention it as it contains no new information - they say "for simplicity, we restrict the discussion to $m \times m$ grids" –  Feb 21 '13 at 14:26
  • Just an information, what is the upper bound for the length of the solutions of a generic $n^2 -1$ instance ? – Marzio De Biasi Feb 22 '13 at 17:05
  • @Vor A very bad upper bound would be the amount of states of the puzzle, which is $\leq (n^2)!$. If you want something smaller, there is a paper (http://larc.unt.edu/ian/pubs/saml.pdf) that presents an algorithm that uses at most $5n^3+\mathcal{O}(n^2)$ steps for a given instance. –  Feb 22 '13 at 18:04
  • @Listing: ok thank you (now I see that even in the Ratner and Warmuth there is an approximation algorithm) – Marzio De Biasi Feb 22 '13 at 18:18
  • 2
    I have written an unpublished implementation of Parberry's $O(n^3)$ algorithm (saml.pdf), adapted to the asymmetric case. It works :-)

    Also, I've been citing Erik Demaine's survey paper in my publications related to the topic. Get it at http://erikdemaine.org/papers/AlgGameTheory_GONC3/; it's a bit newer than the 2008 paper, FWIW.

     – Jonas Kölker Feb 23 '13 at 10:33
  • @JonasKölker That is neat, I will include it into the reference list. I still wonder why the asymmetric case is completely ignored in most publications though. –  Feb 23 '13 at 10:51
  • @Listing: probably no one finds the asymmetric case particularly interesting. Which means you get to break new ground here ;-) – Jonas Kölker Feb 23 '13 at 10:59
  • @JonasKölker: but I think that the fixed height version (even for arbitrary large fixed $q$) is ignored because in that case (dis)proving that the moves minimization problem is NP-complete is much harder than in the unrestricted version :-) – Marzio De Biasi Feb 23 '13 at 11:01
  • Could be. That means you'll break a lot of new ground :D – Jonas Kölker Feb 23 '13 at 11:10
  • @Listing My guess is that fixing any dimension to any constant makes the problem polynomial-time solvable but I do not have solid proof. – Mohammad Al-Turkistany Feb 23 '13 at 11:15
  • @MohammadAl-Turkistany: I'll bet 1$ on NPI :-) – Marzio De Biasi Feb 23 '13 at 11:37
  • 4
    @Vor I offer $50 cash prize for NP-completeness proof :) – Mohammad Al-Turkistany Feb 23 '13 at 11:41
  • 1
    @Vor If you can prove that it is in NPI then you win $1 million from Clay math. – Mohammad Al-Turkistany Feb 23 '13 at 11:43
  • BTW, Is it acceptable to offer cash prizes for solutions? – Mohammad Al-Turkistany Feb 23 '13 at 11:45
  • @MohammadAl-Turkistany: to be precise $999.999 (because I have to pay the 1$ to the one who solved it for me :-))) – Marzio De Biasi Feb 23 '13 at 11:45
  • 1
    @MohammadAl-Turkistany: perhaps a good question for Meta ... – Marzio De Biasi Feb 23 '13 at 11:46
  • @Vor Good one :) – Mohammad Al-Turkistany Feb 23 '13 at 11:49
  • 2
    Related?: http://cstheory.stackexchange.com/questions/783/is-optimally-solving-the-nnn-rubiks-cube-np-hard – Joshua Grochow Feb 27 '13 at 00:06
  • 1
    After a quick look to the paper suggested by Joshua I bet 2$ on P :-) – Marzio De Biasi Feb 27 '13 at 16:45
  • 1
    imho this is not precisely asked & there are 2 different problems. "Listing" refers to an "asymmetric case" ie $p\neq q$. but that is not the same as what he also asks for, "fixed q". suspect/conjecture that the $p \neq q$ case is also NP complete. conjecture that the fixed $q$ case is in P. it would be more helpful to pinpoint what construction/thm/lemma in the ratner/warmuth paper fails to work on the different geometry. the main idea seems to reduce $m \times m$ 2-2-4 SAT ($m$ vars, $m$ clauses) to "REL", a problem of relocation of elements that reside in vertices of eulerian/planar graph – vzn Feb 27 '13 at 17:11
  • 2
    @vzn Sorry if I was not specific enough here - I only want to ask for fixed q, which is a special form of the asymmetric case. – Listing Feb 27 '13 at 17:13
  • further looking, a key construction is in the appendix of ratner/warmuth paper, reducing 1/3 SAT to $m \times m$ 2-2-4 SAT. maybe the rest of the proof will work if that reduction is changed to $m \times n$ 2-2-4 SAT, $m$ clauses, $n$ vars...? – vzn Feb 27 '13 at 18:07
  • 2
    @vzn As previously mentioned I only want to focus on fields with constant height. The transformation which gives us the initial configuration, taking an instance of "REL" seems to produce boards with polynomial height - that is why the proof would not work. – Listing Feb 27 '13 at 18:28

1 Answers1

4

I think that I found a partial (although quite disappointing) answer to my problem:

I stumbled across this paper (2007):

"The Complexity of Three-Dimensional Channel Routing" by Satoshi Tayu and Shuichi Ueno

They show (Theorem 4) that the "3d-channel routing problem" with "2-nets" and dimension $p,q$ can be solved if and only if the corresponding (check article for more details) $p \times q-1$ puzzle can be solved.

Below Theorem 1 they propose some problem they call "2.5-D CHANNEL ROUTING", which is basically "3d-channel routing" with fixed depth $k$. They also say "the complexity of the following problem [2.5-D Channel Routing] is open for any fxed integer $k \geq 2$".

If we knew that the decision version of the $p \times q-1$ puzzle is NP-Complete for some fixed $k \geq 2$ we would also know that 2.5-D Channel Routing is difficult for that $k$, therefore it seems the question can be reduced to some open problem.

It could of course be that the answer to my question would be that $p \times q-1$ puzzle is in P for all fixed $k$, which would still leave their question open (as the general routing doesn't only handle $2$-Nets). Therefore this is no complete answer, it is also rather disappointing that they include no references when claiming that the problem is still open.

Listing
  • 607
  • 5
  • 13