All 2-body systems end up tidally locking each other. In fact, the Earth is slowly going into tidal locking with the Moon, it just takes a lot longer for the larger body to lock with the smaller one (the moon is of course already locked). In your case, it is expected that a binary system of asteroids would be tidally locked.
I simulated the asteroids orbiting the sun at one AU, where the sun has position {0,0,0} and a velocity which offsets that of the asteroids.
Let's assume our asteroids have an average density of $~1000\frac{kg}{m^3}$. Then the mass of asteroid of $3\left(km\right)$ diameter with a volume of $\frac{4}{3}\pi 1.5^3\left(km^3\right)\approx14\left(km^3\right)=14\times10^9\left(m^3\right)$ has a mass of $14\times10^{12}\left(kg\right)$
We can estimate the relative velocity by means of an idealized circular motion, in which case $a=\frac{v^2}{r}$. We also know that the acceleration due to asteroid 2 is $$G\frac{m}{r^2}=6.674\times10^{-11}\left(N \frac{m^2}{kg^2}\right)\frac{20\times10^{12}(kg)}{\left(1.5\times10^4\right)^2(m^2)}=5.93\times10^3\left(\frac{m}{s^2}\right)$$
And thus:
$$v=\sqrt{ar}=\sqrt{1.5\times10^4(m)\times5.93\times10^3\left(\frac{m}{s^2}\right)}=0.3\left(\frac{m}{s}\right)$$
This gives us a good aprroximation, and with some testing, it turns out that $0.4\left(\frac{m}{s}\right)$ gives us a good orbit:
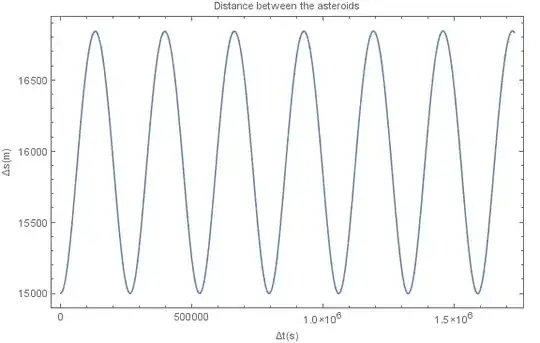
So, let's use the following statistics:
Asteroid 1
Mass: $14\times10^{12}$
Position:$\left(AU,0,0\right)$
Velocity:$\left(0.4\frac{m}{s},29780\frac{m}{s},0\right)$
Asteroid 2
Mass: $20\times10^{12}$
Position:$\left(AU,15\times10^3,0\right)$
Velocity:$\left(0,29780\frac{m}{s},0\right)$
Meaning they have an initial distance and velocity relative to eachother of $\Delta s=13\times10^3$,$\Delta v=0.4\frac{m}{s}$.
Behaviour
Our asteroids have a steady near circular orbit around the sun, the orbit takes about 390 Earth days:

The distance between the asteroids fluctuates slightly, both in the short as long term, this is more realistic than perfectly circular orbits.
The long term fluctuation is due to the influence of the sun, this gives the distance between the asteroids over 2 earth years:
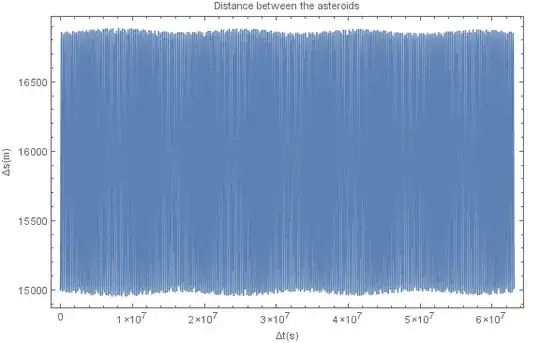
Tidal locking
The asteroids rotate very slowly around eachother, and will almost certainly be tidally locked.
Eccentricity and Stability
This configuration is stable over single digit years, the precise configuration needs to change for stability to be maintained over more years.
For decades long stability, the eccentricity actually seems to decrease, regardless of the initial situation, however when the orbit eccentricity becomes too low (the orbits become highly circular), the orbits become suddenly less stable, here is the plot over 200 years:

As you can see, after 70 years or so, the asteroids start to draw closer together. Increasing velocity accuracy, draws this out,
Let me know if you need anything else, I love this stuff.
My guess is this means it's really difficult to find a stable orbit between such two small objects, however by increasing the accuracy of the velocity, it should be possible for the orbit to be stable for a few thoasand years, though such a configuration would be highly unlikely to occur naturally.



