Centrifugal force effectively counteracts surface gravity making spinning worlds bulge and making gravity at the equator slightly less than at the poles. Hal Clement notably took this to an extreme with the planet Mesklin from Mission of Gravity, with 3g at the equator and around 700g at the poles... but what if we take it to an even greater extreme?
A neutron star spinning Sufficiently Fast should eventually end up with an equatorial bulge that has weak enough gravity for degenerate matter to start "re-inflating". Spin it even faster, and eventually you'll get a normal-matter rim that a human could stand on (while the sky is a series of fully-blurred circular streaks of stars).
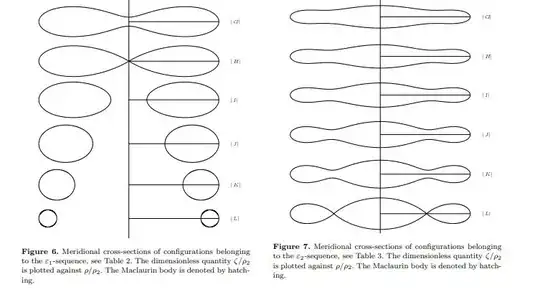
But... what might that actually look like? What's the final shape? Would there actually be room to stand on that equator, or would it be too thin to inhabit? It would be relatively simple to work out the shape of an oblate spheroid of uniform density, or the equipotential surface around a point mass, but this thing is not really close to either ideal.
I realize a fully accurate answer would rely on information about degenerate nuclear matter physics that we just don't have yet, but I'd like to make this as accurate as possible for sci-fi. And if a precise answer is impractical to give, I would still appreciate references that might help me figure it out.