3

There was this question about spacetime with two time dimensions here, but I wonder what could that mean particularly for thermodynamics?

To be more precise, could such a universe (none of dimensions are compactified) have same laws of thermodynamics we have? I'd prefer to keep laws of thermodynamics from a modern physics intact in my fictional universe with two time dimensions, but can I do it in physically consistent manner? If not, what are exact problems?

Nervous Cat
  • 163
  • 4
  • I asked a question about three-dimensional time as a sideways way of permitting an alternative to time travel (because there is more than one dimension of time, you could travel to an otherwise identical alternate reality past, but not your own). In that, the extra time dimensions needed to be independent of our regular causal reality, so they wouldn't affect thermodynamics. I don't THINK it answers your question, though. https://worldbuilding.stackexchange.com/questions/176601/is-three-dimensional-time-consistent-and-paradox-free-for-time-dimension-travele – DWKraus Jan 20 '21 at 02:46
  • 2
    What is the specific worldbuilding issue or problem you're trying to solve here? Try to focus on a particular issue. – elemtilas Jan 20 '21 at 03:11

1 Answers1

1

Scientists have been exploring the consequences of having more dimensions, both on the space-side N and on the time-side T.

According to this wikipedia page

If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that protons and electrons would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.) N = 1 and T = 3 has the peculiar property that the speed of light in a vacuum is a lower bound on the velocity of matter; all matter consists of tachyons

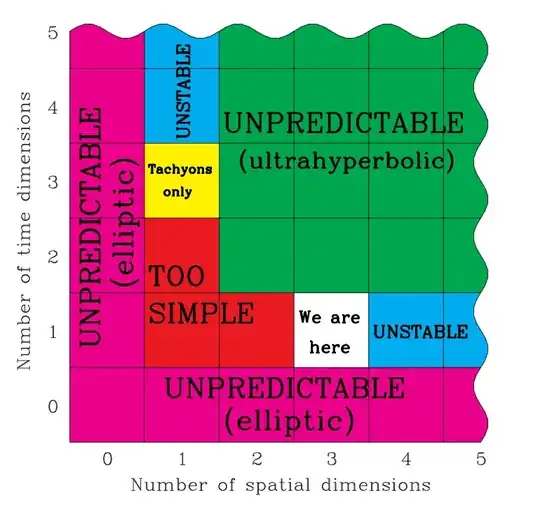
enter image description here

It seems therefore that, generally speaking, we cannot know. Even if we can come with some differential equations, those won't help to predict the story and the evolution of the modeled system.

Also this paper seems to suggests that in certain conditions first and second law of thermodynamics can be derived, but the second law cannot be satisfied.

In this work, we have considered the Vaidya spacetime in null radiating fluid with perfect fluid in higher dimension and have found the solution for barotropic fluid. We have shown that the Einstein's field equations can be obtained from Unified first law i.e., field equations and unified first law are equivalent. The first law of thermodynamics has also been constructed by Unified first law. From this, the variation of entropy function has been derived on the horizon. The variation of entropy function inside the horizon has been derived using Gibb's law of thermodynamics. So the total variation of entropy function has been constructed at apparent and event horizons both. If we do not assume the first law, then the entropy on the both horizons can be considered by area law and the variation of total entropy has been found at both the horizons. Also the validity of generalized second law (GSL) of thermodynamics has been examined at both apparent and event horizons by using the first law and the area law separately. When we use first law of thermodynamics and Bekenstein-Hawking area law of thermodynamics, the GSL for apparent horizon in any dimensions are satisfied, but the GSL for event horizon can not be satisfied in any dimensions.

L.Dutch
  • 286,075
  • 58
  • 587
  • 1,230