Geometrie afină

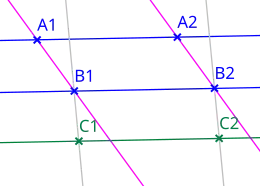
În geometria afină, se poate folosi axioma lui Playfair pentru a găsi linia ce trece prin C1 și paralelă cu B1B2, și pentru a găsi linia ce trece prin B2 și paralelă cu B1C1: intersecția lor C2 este rezultatul translației indicate.

Geometrie
Proiecția unei sfere pe un plan
Glosar Istorie
Ramuri Euclidiană Neeuclidiană Eliptică Sferică Hiperbolică Nearhimedică Proiectivă Afină Sintetică Analitică Algebrică Aritmetică Diofantică Diferențială Riemanniană Simplectică Diferențială discretă Complexă Finită Discretă/Combinatorică Digitală Convexă Computațională Fractal De incidență
Concepte Caracteristici Dimensiune Construcții cu rigla și compasul Unghi Curbă Diagonală Ortogonalitate (Perpendicularitate) Paralelism Congruență Asemănare Simetrie
Zerodimensional Punct
Unidimensional Dreaptă Segment Lungime
Bidimensional Plan Arie Poligon Triunghi Înălțime Ipotenuză Teorema lui Pitagora Paralelogram Pătrat Dreptunghi Romb Patrulater Romboid Trapez Conică Cerc Circumferință Diametru Rază Disc Elipsă Hiperbolă Parabolă
Tridimensional Volum Cub Cuboid Cilindru Piramidă Bilă Sferă Elipsoid Hiperboloid Paraboloid
Cvadri- și n-dimensional Simplex Hipercub Tesseract Hipersferă

Geometria afină este un tip de geometrie care studiază paralelismul. În această geometrie, a treia și respectiv a patra axiomă a lui Euclid nu sunt luate în considerare. Raportat la geometria euclidiană se renunță la noțiunile de distanță și măsură a unghiurilor.

A fost studiată pentru prima dată de Leonhard Euler. În 1748, Euler a introdus termenul afin^[1][2] (latină affinis, înrudit) în lucrarea sa Introductio in analysin infinitorum.

Referințe

Vezi și

• Geometrie proiectivă
• Spațiu afin
• Teorema lui Ceva

Legături externe

• Curs de geometrie afină Arhivat în 19 februarie 2018, la Wayback Machine.
• la math wikia