Progresie armonică

În matematică o progresie armonică[lower-alpha 1] este un șir ai cărui termeni sunt inversele termenilor unei progresii aritmetice.

Pentru termenul muzical, vedeți Progresie de acorduri.

Primii zece termeni ai progresiei armonice

a_{n}={\tfrac {1}{n}}

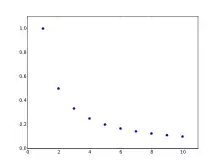
Echivalent, un șir este o progresie armonică când fiecare termen (cu excepția capetelor) este media armonică a termenilor vecini. De aici vine și denumirea progresiei.

O a treia caracterizare echivalentă este o secvență infinită a formei

{\frac {1}{a}},\ {\frac {1}{a+d}},\ {\frac {1}{a+2d}},\ {\frac {1}{a+3d}},\cdots ,

unde a este nenul iar −a/d nu este un număr natural sau un șir finit de forma

{\frac {1}{a}},\ {\frac {1}{a+d}},\ {\frac {1}{a+2d}},\ {\frac {1}{a+3d}},\cdots ,\ {\frac {1}{a+kd}},

unde a este nenul, k este un număr natural iar −a/d nu este un număr natural sau este mai mare decât k.

Exemple

1, 1/2, 1/3, 1/4, 1/5, 1/6, uneori numit șirul armonic
12, 6, 4, 3, ${\tfrac {12}{5}}$ , 2, … , ${\tfrac {12}{n}}$ , …
30, −30, −10, −6, − ${\tfrac {30}{7}}$ , … , ${\tfrac {10}{1-{\tfrac {2n}{3}}}}$
10, 30, −30, −10, −6, − , … , ${\tfrac {10}{1-{\tfrac {2(n-1)}{3}}}}$

Suma progresiilor armonice

Suma progresiilor armonice infinite tinde la infinit.

Nu este posibil ca suma unei progresii armonice de fracții cu numărătorul 1 (altul decât cazul banal în care a = 1 și k = 0) să fie un număr întreg. Motivul este că, în mod necesar, cel puțin un numitor al progresiei va fi divizibil cu un număr prim care nu divide niciun alt numitor.[1]

Utilizarea în geometrie

Dacă punctele coliniare A, B, C și D sunt astfel încât D este conjugatul armonic al lui C față de A și B, atunci distanțele de la oricare dintre aceste puncte la cele trei puncte rămase formează o progresie armonică.[2][3] În particular, oricare din șirurile AC, AB, AD; BC, BA, BD; CA, CD, CB și DA, DC, DB sunt progresii armonice, unde fiecare dintre distanțe este definită de orientarea fixă a liniei (nu neapărat dreaptă, distanțele măsurându-se pe linie).

Într-un triunghi, dacă înălțimile sunt în progresie aritmetică, atunci laturile sunt în progresie armonică.

Note explicative

Expresiile șir armonic și secvență armonică nu sunt uzuale în terminologia matematică românească, ele se întâlnesc exclusiv în domeniul muzical.

Note

hu Erdős, P. (1932), „Egy Kürschák-féle elemi számelméleti tétel általánosítása” [Generalization of an elementary number-theoretic theorem of Kürschák] (PDF), Mat. Fiz. Lapok (în Hungarian), 39: 17–24. Citat de Graham, Ronald L. (2013), „Paul Erdős and Egyptian fractions”, Erdős centennial, Bolyai Soc. Math. Stud., 25, János Bolyai Math. Soc., Budapest, pp. 289–309, CiteSeerX 10.1.1.300.91 , doi:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6, MR 3203600
en Richard Townsend (1865), Chapters on the modern geometry of the point, line, and circle, Vol. II, p. 24
en John Alexander Third (1898), Modern geometry of the point, straight line, and circle: an elementary treatise p. 44

Bibliografie

en Stan Gibilisco, Norman H. Crowhurst (2007), Mastering Technical Mathematics, p. 221
en Chemical Rubber Company (1974), Standard mathematical tables, p. 102
en Webster Wells (1897), Essentials of algebra for secondary schools, p. 307

Vezi și

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Expresiile șir armonic și secvență armonică nu sunt uzuale în terminologia matematică românească, ele se întâlnesc exclusiv în domeniul muzical.

[2] u Erdős, P. (1932), „Egy Kürschák-féle elemi számelméleti tétel általánosítása” [Generalization of an elementary number-theoretic theorem of Kürschák] (PDF), Mat. Fiz. Lapok (în Hungarian), 39: 17–24. Citat de Graham, Ronald L. (2013), „Paul Erdős and Egyptian fractions”, Erdős centennial, Bolyai Soc. Math. Stud., 25, János Bolyai Math. Soc., Budapest, pp. 289–309, CiteSeerX 10.1.1.300.91 , doi:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6, MR 3203600

[3] Richard Townsend (1865), Chapters on the modern geometry of the point, line, and circle, Vol. II, p. 24

[4] John Alexander Third (1898), Modern geometry of the point, straight line, and circle: an elementary treatise p. 44