Problema ghiulelelor

În matematica numerelor figurative problema ghiulelor tratează numerele care sunt atât pătratice, cât și piramidale pătratice. Problema poate fi formulată astfel: având în vedere un aranjament pătrat de ghiulele, pentru care pătrate aceste ghiulele pot fi aranjate într-o piramidă pătrată. Echivalent, care pătrate sunt și suma pătratelor consecutive, începând de la 1.

91 de ghiulele aranjate într-o piramidă pătrată. Deși 91 este un număr piramidal pătratic, el nu este și un pătrat perfect, deci nu este o soluție la problema ghiulelelor.

Formularea ca ecuație diofantică

Când ghiulele sunt stivuite într-un cadru pătrat, numărul lor este un număr piramidal pătratic. Thomas Harriot a dat o formulă pentru acest număr în jurul anului 1587, răspunzând la o întrebare adresată de Sir Walter Raleigh în expediția lor în America.[1] Édouard Lucas a formulat problema ghiulelelor prin ecuația diofantică

sau

4900 de ghiulele pot fi aranjate fie ca un pătrat cu latura de 70, fie ca o piramidă pătrată cu latura de 24

Lucas a emis conjectura că singurele soluții ale acestei ecuații sunt N = 1, M = 1 și N = 24, M = 70, care corespund la 1, respectiv 4900 de ghiulele. În 1918 G. N. Watson a demonstrat conjectura folosind funcții eliptice. Ulterior au fost publicate și demonstrații elementare.[2][3]

Aplicații

Soluția N = 24, M = 70 poate fi folosită pentru generarea unei latice Leech. Rezultatul are importanță în teoria coardelor bosonice în 26 de dimensiuni.[4]

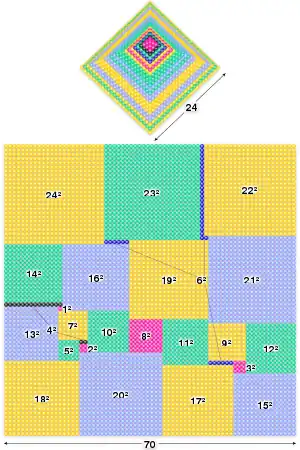
Deși este posibilă acoperirea unui pătrat cu pătrate inegale, asta nu se poate realiza cu soluția problemei ghiulelelor. Suma ariilor pătratelor cu laturile de la 1 la 24 este egală cu aria pătratului cu latura de 70, dar ele nu pot fi aranjate pentru a-l pava.

Probleme asemănătoare

Singurele numere care sunt simultan triunghiulare și piramidale pătrate sunt 1, 55, 91 și 208335.[5][6]

În afară de soluția banală 1, nu există numere care să fie simultan tetraedrice și piramidale pătratice.[6]

Note
  1. en David Darling. „Cannonball Problem”. The Internet Encyclopedia of Science.
  2. en Ma, D. G. (). „An Elementary Proof of the Solutions to the Diophantine Equation ”. Sichuan Daxue Xuebao. 4: 107–116.
  3. en Anglin, W. S. (). „The Square Pyramid Puzzle”. American Mathematical Monthly. 97 (2): 120–124. doi:10.2307/2323911. JSTOR 2323911.
  4. en „week95”. Math.ucr.edu. . Accesat în .
  5. Șirul A039596 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
  6. en Eric W. Weisstein, Square Pyramidal Number la MathWorld.

Legături externe
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.