Icositetraedru
În geometrie un icositetraedru[1][2] este un poliedru cu 24 de fețe. Există numeroase forme simetrice, iar unele dintre cele foarte simetrice au simetrie icosaedrică chirală
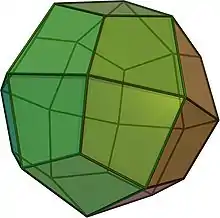 Convex, Catalan |
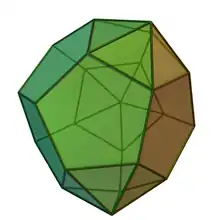 Convex, Johnson |
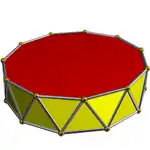 Convex, antiprismă |
 Neconvex, stelat |
Exemple de icositetraedre
Convexe
Există patru poliedre Catalan cu câte 24 de fețe:[3]
| Imagine | Denumire | Tipul fețelor |
|---|---|---|
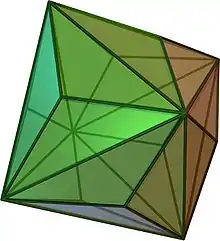 | Octaedru triakis | triunghiuri isoscele |
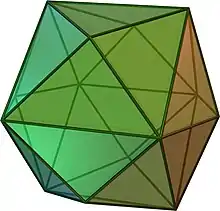 | Hexaedru tetrakis | triunghiuri isoscele |
 | Icositetraedru romboidal | romboizi |
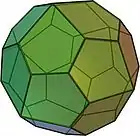 | Icositetraedru pentagonal | pentagoane neregulate |
Există două poliedre Johnson cu câte 24 de fețe:[4]
| Imagine | Denumire | Tipul fețelor |
|---|---|---|
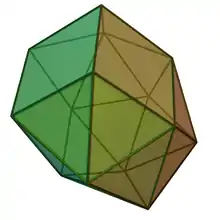 | Hebesfenmegacoroană | triunghiuri regulate și pătrate |
 | Dodecaedru triaugmentat | triunghiuri regulate și pentagoane |
Alte poliedre convexe
- Prismă icosidigonală (bazele sunt 22-goane)
- Trunchi icosidigonal (bazele sunt 22-goane)
- Antiprismă endecagonală (bazele sunt 11-goane)
- Piramidă icositrigonală (baza este un 23-gon)
- Bipiramidă dodecagonală
- Cupolă endecagonală
Neconvexe
Stelate
| Imagine | Denumire | Tipul fețelor |
|---|---|---|
 | Micul rombihexacron | patrulater autointersectat |
 | Marele rombihexacron | patrulater autointersectat |
 | Micul icositetraedru hexacronic | patrulater autointersectat |
 | Marele icositetraedru hexacronic | romboizi convecși |
 | Marele icositetraedru romboidal | romboizi concavi |
 | Marele icositetraedru trakis | triunghiuri isoscele |
Note
- „icositetraedru” la DEX online
- en „Greek numerical prefixes”.
- fr Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865
- en Johnson, Norman W. (). „Convex Solids with Regular Faces”. Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603. Conține enumerarea celor 92 de poliedre și conjectura că nu există altele.
Bibliografie
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.