Funcția beta
În matematică, funcția beta este o funcție specială, înrudită cu funcția gamma, întâlnită în calcularea mai multor integrale definite. Este o funcție cu două variabile și este definită pentru și astfel:
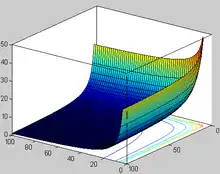
Graficul funcției B(x,y) cu argumente reale pozitive.
Definiții alternative
Ca urmare,
Această definiție este valabilă și pentru numerele complexe care au părțile reale pozitive și a fost dată de către Euler în 1730. Numele de funcție beta a fost introdus de către Jacques Philippe Marie Binet în 1839, el aducând mari contribuții la studiul acesteia.
Funcția beta este simetrică și și poate fi calculată cu ajutorul funcției gamma datorită proprietății:
Proprietate
Fie și . Atunci,
Valori particulare ale funcției beta
- ,
- ,
- ,
- ,
- ,
Pentru , avem:
- ,
- .
Legături externe
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.