Hyperbolic growth
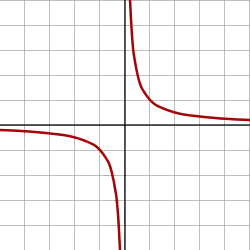
When a quantity grows towards a singularity under a finite variation (a "finite-time singularity") it is said to undergo hyperbolic growth.[1] More precisely, the reciprocal function has a hyperbola as a graph, and has a singularity at 0, meaning that the limit as is infinite: any similar graph is said to exhibit hyperbolic growth.
Description
If the output of a function is inversely proportional to its input, or inversely proportional to the difference from a given value , the function will exhibit hyperbolic growth, with a singularity at .
In the real world hyperbolic growth is created by certain non-linear positive feedback mechanisms.[2]
Comparisons with other growth functions

Like exponential growth and logistic growth, hyperbolic growth is highly nonlinear, but differs in important respects. These functions can be confused, as exponential growth, hyperbolic growth, and the first half of logistic growth are convex functions; however their asymptotic behavior (behavior as input gets large) differs dramatically:
- logistic growth is constrained (has a finite limit, even as time goes to infinity),
- exponential growth grows to infinity as time goes to infinity (but is always finite for finite time),
- hyperbolic growth has a singularity in finite time (grows to infinity at a finite time).
Applications
Global macrodevelopment
A 1960 issue of Science magazine included an article by Heinz von Foerster and his colleagues, P. M. Mora and L. W. Amiot, proposing an equation representing the best fit to the historical data on the Earth's population available in 1958:
Fifty years ago, Science published a study with the provocative title “Doomsday: Friday, 13 November, A.D. 2026”. It fitted world population during the previous two millennia with P = 179 × 109/(2026.9 − t)0.99. This “quasi-hyperbolic” equation (hyperbolic having exponent 1.00 in the denominator) projected to infinite population in 2026—and to an imaginary one thereafter.
- —Taagepera, Rein. A world population growth model: Interaction with Earth's carrying capacity and technology in limited space Technological Forecasting and Social Change, v. 82, February 2014, pp. 34–41
%252C_OWID.svg.png)
In 1975, von Hoerner suggested that von Foerster's doomsday equation can be written, without a significant loss of accuracy, in a simplified hyperbolic form (i.e. with the exponent in the denominator assumed to be 1.00):
where
- 2026.9 (more precisely, 13 November 2026 AD) is the date of the so-called "demographic singularity"[3] and von Foerster's 115th anniversary;
- t is the number of a year of the Gregorian calendar.[4]
Despite its simplicity, von Foerster's equation is very accurate in the range from 4,000,000 BP[5] to 1997 AD. For example, the doomsday equation (developed in 1958, when the Earth's population was 2,911,249,671[6]) predicts a population of 5,986,622,074 for the beginning of the year 1997:
The actual figure was 5,924,787,816.[6]
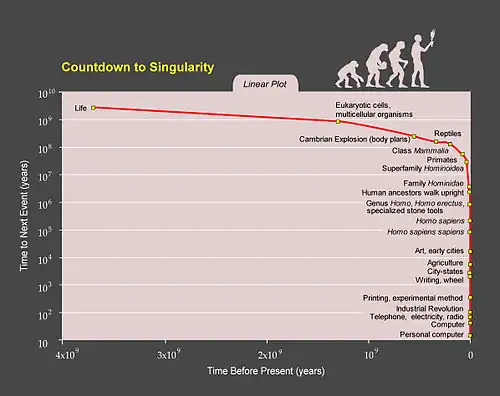
Having analyzed the timing of the events plotted on Ray Kurzweil's "Countdown to Singularity" graph, Andrey Korotayev arrived at the following best-fit equation:
where
- "speed of sociotechnological progress" is the number of sociotechnological phase transitions per a unit of time;
- 2029 (more precisely, the beginning of the year 2029 AD) is the date of sociotechnological singularity;
- t is the number of a year of the Gregorian calendar.[3]
Korotayev also analized the timing of the events on the list of sociotechnological phase transition points independently compiled by Alexander Panov, and arrived at the following best-fit equation:
where
- "speed of sociotechnological progress" is the number of sociotechnological phase transitions per a unit of time;
- 2027 (more precisely, the beginning of the year 2027 AD) is the date of sociotechnological singularity;
- t is the number of a year of the Gregorian calendar.[3]
Korotayev discovered that these two equations are entirely identical with von Foerster's doomsday equation describing the world population growth. Both empirical and mathematical analyses indicate that all the three hyperbolic equations describe the same global macrodevelopmental process, in which demography is indivisibly combined with technology.[7] It can be set forth as follows: technological advance → increase in the carrying capacity of the Earth → population growth → more potential inventors → acceleration of technological advance → faster growth of the Earth's carrying capacity → faster population growth → faster growth of the number of potential inventors → faster technological advance → faster growth of the Earth's carrying capacity, and so on.[8]
Lorentz factor
The Lorentz factor γ is defined as[9] where
- v is the relative velocity between inertial reference frames;
- c is the speed of light in vacuum;
- β is the ratio of v to c, or the speed in units of c.
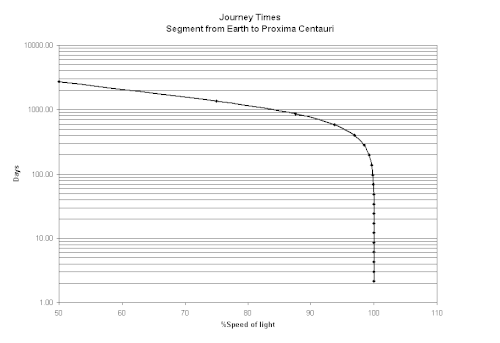
Proxima Centauri is approximately 4.27 light-years away from the Earth. From a terrestrial observer's perspective, a traveller would cover the distance to Proxima Centauri in approximately 8.54 years at half the speed of light. However, due to the Lorentz factor, the time experienced by the traveller would be shorter:
The following graph shows the journey times for twenty runs to Proxima Centauri from the ship viewpoint. Notice that as speeds approach the speed of light, the journey times reduce dramatically, even though the actual increments in speed appear slight. On the 20th run, at 1048575/1048576 of the speed of light, the distance shrinks to 0.0059 light-years and the traveller experiences a journey time of 2.15 days. Whereas to those on Earth the ship looks almost ‘frozen’ and the journey still takes 4.27 years, plus a couple of days.
The equation describing the growth of the Lorentz factor with speed is unmistakably hyperbolic, so the Lorentz factor of a spaceship, subjected to even a small but constant accelerating force, must become infinite in a finite time. This requirement is met by assuming that a translationally accelerating spaceship loses its rest mass (which is the spaceship's resistance to its further translational acceleration along the path of flight): where
- m0 is rest mass (resistance to longitudinal acceleration);
- mrel is relativistic mass (resistance to transverse acceleration).[10]
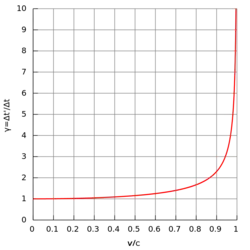
At v = 0, the magnitude of the Lorentz factor is At v = 0.5 c, the magnitude of the Lorentz factor is At v = 0.999 c, the magnitude of the Lorentz factor is Following this pattern, the spaceship will, after a finite time, turn into a beam of photons:
Photons may be regarded as limiting particles whose rest mass has become zero while their Lorentz factor has become infinite.
- —Rindler, W. Essential Relativity: Special, General, and Cosmological Springer, 2013, p. 115
The light-speed spaceship will then cover the remaining distance to its destination in a zero proper time:
Since when traveling at the speed of light no apparent time elapses, the spacecraft would arrive instantly and simultaneously at all locations along the path of flight. Thus to the crew on the spacecraft, all spatial separations would collapse to zero along this path‑of‑flight. There is no relativistic dilatation, as all spatial separations are transverse to a light-speed spacecraft's flight. <...> Thus the spacecraft would disappear after reaching light speed, followed immediately by its reappearance trillions of miles away in the proximity of the target star, when the spacecraft returns to sub-light speed, Figure 9.6.
- —Czysz, Paul A.; Bruno, Claudio. Future Spacecraft Propulsion Systems Springer, 2006, p. 429
The universe's matter is falling into the universe's gravitational field:
Gravity rules. The moon orbiting Earth, matter falling into black holes, and the overall structure of the universe are dominated by gravity.
- —Seeds, Michael A.; Backman, Dana. Foundations of Astronomy Cengage Learning, 2010, p. 75
Consequently, the universe's matter accelerates to ever greater speeds, so that its Lorentz factor hyperbolically increases to infinity, while its rest mass hyperbolically vanishes:
As we go forwards in time, material weight continually changes into radiation. Conversely, as we go backwards in time, the total material weight of the universe must continually increase.
- —Jeans, James Hopwood. The Universe Around Us CUP, 1930, pp. 330–32
At the end of the hyperbolic growth of its Lorentz factor, the universe's matter attains the speed of light:
‘It all just seemed unbelievably boring to me,’ Penrose says. Then he found something interesting within it: at the very end of the universe, the only remaining particles will be massless. That means everything that exists will travel at the speed of light, making the flow of time meaningless.
- —Brooks, Michael. Roger Penrose: Non-stop cosmos, non-stop career New Scientist, 10 March 2010
So, the universe will eventually consist of relativistic kinetic energy, which is negative, i.e. hierarchically binding/enslaving:
A beam of negative energy that travels into the past can be generated by the acceleration of the source to high speeds.
- —Skinner, Ray. Relativity for Scientists and Engineers Courier Corporation, 2014, pp. 188–89
It is seen that the relativistic kinetic energy is always negative and therefore will lower the energy levels of a bound system.
- —Ruei, K. H. Quantum Theory of Particles and Fields Vol. 2, University Press, 1971, p. 39
This hierarchically binding/enslaving negative energy is the universe's spirit or information:
Remember, more binding energy means the system is more bound—has greater negative energy.
- —Shu, Frank. The Physical Universe: An Introduction to Astronomy University Science Books, 1982, p. 66
The Spirit is the binding energy expressed by the word re-ligio/religion—a word that itself reflects the brokenness and fragmentation of the universe, that God is trying to heal.
- —Grey, Mary C. Introducing Feminist Images of God Sheffield Academic Press, 2001, p. 84
Szilard's explanation was accepted by the physics community, and information was accepted as a scientific concept, defined by its statistical‑mechanical properties as a kind of negative energy that introduced order into a system.
- —Aspray, William. The Origins of John von Neumann's Theory of Automata In "Proceedings of the Summer Research Institute on the legacy of John von Neumann held at Hofstra University, Hempstead, New York, May 29–June 4, 1988". American Mathematical Society, 1990, p. 291
Thus, the hyperbolic growth of the Lorentz factor of the universe's matter hierarchically binds/enslaves or, which is the same, animates/informs the universe's matter. The sociotechnological singularity of the terrestrial animated/informed matter, expected at the end of the year 2026 AD (see Global macrodevelopment) will signify that the Lorentz factor of the universe's matter has become infinite—since the end of the year 2026 AD, the universe's matter will be falling into the universe's animating/informing gravitational field (which is the gradient of matter's negative-energiedness, animateness, informedness) at the speed of light:
The negative energy of the gravitational field is what allows negative entropy, equivalent to information, to grow, making the Universe a more complicated and interesting place.
- —Gribbin, John. In Search of the Multiverse Penguin, 2009, p. 131


Queuing theory
Another example of hyperbolic growth can be found in queueing theory: the average waiting time of randomly arriving customers grows hyperbolically as a function of the average load ratio of the server. The singularity in this case occurs when the average amount of work arriving to the server equals the server's processing capacity. If the processing needs exceed the server's capacity, then there is no well-defined average waiting time, as the queue can grow without bound. A practical implication of this particular example is that for highly loaded queuing systems the average waiting time can be extremely sensitive to the processing capacity.
Enzyme kinetics
A further practical example of hyperbolic growth can be found in enzyme kinetics. When the rate of reaction (termed velocity) between an enzyme and substrate is plotted against various concentrations of the substrate, a hyperbolic plot is obtained for many simpler systems. When this happens, the enzyme is said to follow Michaelis-Menten kinetics.
Mathematical example
The function
exhibits hyperbolic growth with a singularity at time : in the limit as , the function goes to infinity.
More generally, the function
exhibits hyperbolic growth, where is a scale factor.
Note that this algebraic function can be regarded as an analytical solution for the function's differential:[12]
This means that with hyperbolic growth the absolute growth rate of the variable x in the moment t is proportional to the square of the value of x in the moment t.
Respectively, the quadratic-hyperbolic function looks as follows:
See also
Notes
- ↑ See, e.g., Korotayev A., Malkov A., Khaltourina D. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: URSS Publishers, 2006. P. 19-20.
- ↑ See, e.g., Alexander V. Markov, and Andrey V. Korotayev (2007). "Phanerozoic marine biodiversity follows a hyperbolic trend". Palaeoworld. Volume 16. Issue 4. Pages 311-318.
- 1 2 3 Korotayev, Andrey. The 21st Century Singularity and its Big History Implications: A re-analysis Journal of Big History, II(3), June 2018, pp. 73–119
- ↑ Korotayev, Andrey. The 21st Century Singularity and its Big History Implications: A re-analysis Journal of Big History, II(3), June 2018, pp. 73–119. "We have already mentioned that, as was the case with equations (8) and (9) above, in von Foerster’s Eq. (13) the denominator’s exponent (0.99) turns out to be only negligibly different from 1, and as was already suggested by von Hoerner (1975) and Kapitza (1992, 1999), it can be written more succinctly as Nt = C/(t* − t)."
- ↑ Korotayev, Andrey. "The 21st Century Singularity and its Big History Implications: A re-analysis". Journal of Big History, II(3), June 2018, pp. 73–119. "Note that von Foerster and his colleagues detected the hyperbolic pattern of world population growth for 1 CE –1958 CE; later it was shown that this pattern continued for a few years after 1958, and also that it can be traced for many millennia BCE (Kapitza 1996a, 1996b, 1999; Kremer 1993; Tsirel 2004; Podlazov 2000, 2001, 2002; Korotayev, Malkov, Khaltourina 2006a, 2006b). In fact Kremer (1993) claims that this pattern is traced since 1,000,000 BP, whereas Kapitza (1996a, 1996b, 2003, 2006, 2010) even insists that it can be found since 4,000,000 BP."
- 1 2 World Population by Year Worldometer
- ↑ Korotayev, Andrey. The 21st Century Singularity and its Big History Implications: A re-analysis Journal of Big History, II(3), June 2018, pp. 73–119. "In the Big History context it is definitely of great significance that Eq. (5) describing the global acceleration of the macroevolutionary development rates and Eq. (14) describing the world population growth are entirely identical. What is more, both empirical and mathematical analyses indicate that there is a rather deep substantial connection between those two equations, that they describe two different aspects of the same global macroevolutionary process (see Appendix 1 below)."
- ↑ Introduction to Social Macrodynamics. Archived 10 February 2012 at the Wayback Machine. Andrey Korotayev et al. For a rigorous mathematical analysis of this issue, see "A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE". Archived 17 February 2019 at the Wayback Machine.
- ↑ Forshaw, Jeffrey; Smith, Gavin (2014). Dynamics and Relativity. John Wiley & Sons. ISBN 978-1-118-93329-9.
- ↑ Chaichian, Masud; Merches, Ioan; Radu, Daniel; Tureanu, Anca. Electrodynamics: An Intensive Course Springer, 2016, p. 404. "The concepts of longitudinal and transverse mass of the electron were introduced by Lorentz. in 1904, in his paper ‘Electromagnetic Phenomena in a System Moving with Any Velocity Less than That of Light’, in Proceedings of the Royal Academy of Amsterdam 6 (1904): 809. The so-called ‘transverse mass’ is traditionally named relativistic mass."
- ↑ Rindler, W. Essential Relativity: Special, General, and Cosmological Springer, 2013, p. 115. "Photons may be regarded as limiting particles whose rest mass has become zero while their Lorentz factor has become infinite."
- ↑ See, e.g., Korotayev A., Malkov A., Khaltourina D. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: URSS Publishers, 2006. P. 118-123.
References
- Alexander V. Markov, and Andrey V. Korotayev (2007). "Phanerozoic marine biodiversity follows a hyperbolic trend". Palaeoworld. Volume 16. Issue 4. Pages 311-318].
- Kremer, Michael. 1993. "Population Growth and Technological Change: One Million B.C. to 1990," The Quarterly Journal of Economics 108(3): 681-716.
- Korotayev A., Malkov A., Khaltourina D. 2006. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: URSS. ISBN 5-484-00414-4 .
- Rein Taagepera (1979) People, skills, and resources: An interaction model for world population growth. Technological Forecasting and Social Change 13, 13-30.