I see no elephant, and I assure you I looked very carefully.
In order to make TeX usable, symbols must get a name. The LaTeX names are based mostly on those given by Knuth. Some of them are “agnostic”, such as \otimes or \vert, others reflect common usages.
The \cong symbol is frequently used in elementary geometry to denote “congruence”, according to Hilbert's school. It is also used in higher algebra to denote isomorphism.
On the other hand, \equiv is frequently used to denote “complete identity” (not something I like, but you see f\equiv g to denote that the functions f and g are the same, that is, they take on the same value at every point of their domains, where my algebra background would dictate f=g). It is also used in connection with Gauss congruences over the integers.
Knuth made a decision, which we may not agree with. It's too late for complaining, anyway, because thousands of documents have used \cong for denoting isomorphism.
If you're not satisfied by the semantics, define your own aliases:
\NewCommandCopy{\isom}{\cong}
\NewCommandCopy{\ceq}{\equiv}
\RenewCommandCopy{\cong}{\equiv}
although I discourage from doing the last one, because you risk misunderstandings if you share your source with coauthors.
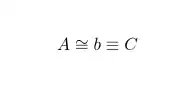
\newcommand\isomorph{\cong}. Different symbols means different things in different fields. – daleif Jan 18 '24 at 11:21isomorphor evenmorphneeds arrows! – yannisl Jan 18 '24 at 11:45Approximately Equal To. The symbol is often used for congruence of geometrical objects, see e.g. https://en.wikipedia.org/wiki/Congruence_(geometry). The second (2261) is calledIdentical Toand a similar symbol U+2263 (≣) isStrickly Equivalent To. So imho the default LaTeX names are fine. – Ulrike Fischer Jan 18 '24 at 12:22