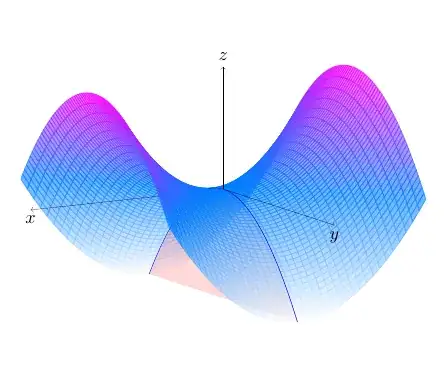
One solution would be to split the paraboloid in two, to achieve some sort of layering. I did the same thing with the coordinate axes.
I modified the code according to @hpekristiansen kind remark concerning the compatibility of the coordinate systems of pdfplots and tikz.
The code
\documentclass[11pt, margin=10pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.17}
\begin{document}
\begin{tikzpicture}
\pgfplotsset{set layers}
\begin{axis}view={150}{12}, axis lines=none]
\addplot3[
surf,
colormap/cool,
shader=flat,
opacity=.6,
domain=-4:4,
domain y=-4:0,
samples=40,
clip=false
] {x^2 -y^2};
% plane section x = 0
\addplot3[%
draw=blue, very thin,
fill=red, fill opacity=.15,
domain=-4:4,
samples y=0
] (0, x, {-x^2});
\draw[ultra thin, ->] (0, 0, 0) -- (6, 0, 0)
node[below, text=black, scale=.8] {$x$};
\addplot3[
surf,
colormap/cool,
shader=flat,
opacity=.6,
domain=-4:4,
domain y=0:4,
samples=40,
clip=false
] {x^2 -y^2};
\addplot3[%
draw=blue, very thin,
domain=0:4,
samples y=0
] (0, x, {-x^2});
\draw[ultra thin, ->] (0, 0, 0) -- (0, 0, 18)
node[above, text=black, scale=.8] {$z$};
\draw[ultra thin, ->] (0, 0, 0) -- (0, 6, 0)
node[below, text=black, scale=.8] {$y$};
\end{axis}
\end{tikzpicture}
\end{document}
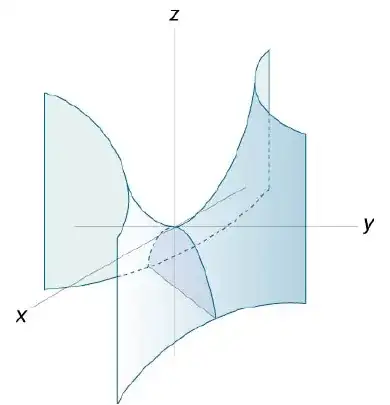

addplot3withsurfdraws the graph of a function defined on a rectangle. In your attached image, the surface is such a graph but with theOzaxis clipped. I don't know if this is possible withaddplot3. In case it is not and you really need that type of representation, I guess you have to do it directly in TikZ where you control the domain of the parametrization (for example the y domain will depend of each x in the x domain). – Daniel N Nov 14 '23 at 05:51