8

I need to draw an isosceles trapezoid with perpendicular diagonals, but I am not sure where to start. Here is my code for a square with perpendicular diagonals (if it is even helpful). 

\begin{tikzpicture}[scale=5.5]
    \coordinate[label=left:$W$]  (W) at (0,0);
    \coordinate[label=right:$X$]  (X) at (1,0);
    \coordinate[label=:$Y$]  (Y) at (1, 1);
    \coordinate[label=:$Z$]  (Z) at (0, 1);
    \coordinate[label=:$O$]  (O) at (0.5, 0.5);
    \draw[] (W)--(X)--(Y)--(Z)--(W)--(Y)--(Z)--(X);
    \draw (O) -- node[sloped] {$\|$} (Y);
    \draw (O) -- node[sloped] {$\|$} (Z);
    \draw (O) -- node[sloped] {$\|$} (X);
    \draw (O) -- node[sloped] {$\|$} (W);
\end{tikzpicture}

Would I have to mathematically find the coordinates of one such trapezoid or is there another way to do it? All help is appreciated!

M. C.
  • 281
  • How would I implement it? I just learned Latex, so I am a complete beginner. – M. C. Jan 10 '19 at 18:17
  • Remember that not any such trapezium has such diagonals. You need to identify under such conditions it has. – Sigur Jan 10 '19 at 18:24
  • Observe that the diagonals determine an isosceles right triangle. – Sigur Jan 10 '19 at 18:26
  • Yes, I checked the code you wrote and it works out well. I guess my problem statement was a bit unclear. Here is what I meant to say: I need a trapezoid with equal base angles and hence equal left and right side lengths. I also want the diagonals to be drawn and to be perpendicular. – M. C. Jan 10 '19 at 18:30
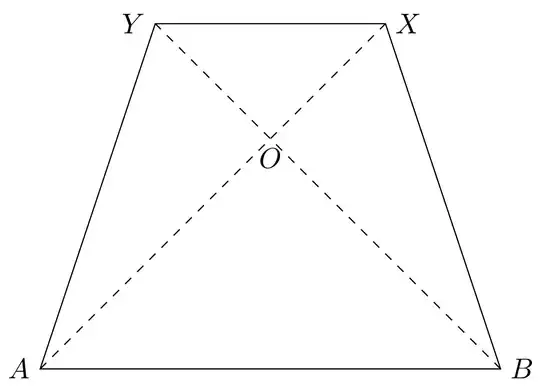
  • @M.C., so that is the case. If trapezium has congruent base angles so ABO should be like that. But, if you want to specify the base angles, so that is another history. – Sigur Jan 10 '19 at 19:06
  • As any trapezoid with perpendicular diagonals must be an isosceles trapezoid so the title can be simplified as "Drawing a trapezoid with perpendicular diagonals". We can save more keystrokes. – Display Name Jan 10 '19 at 21:53

3 Answers3

6

Let ABXY be an isosceles trapezium with perpendicular diagonals AX and BY.

Then, the triangle AOB is isosceles and right at O (ie., the angle at O is right). So, the base angles should have 45 degrees.

Since AB and XY are parallel, to construct the trapezium it is enough to choose the lengths r_1 = OX and r_2 = OA.

If the origin of the coordinate system is O=(0,0) then the vertices can be given in polar coordinates by:

A=(-135:r_2)    B=(- 45:r_2)     X=( 45:r_1)     Y=(135:r_1)

enter image description here

Below, the MWE where the commands 

\newcommand{\radioi}{1cm}
\newcommand{\radioii}{2cm}

determines the radius r_1 and r_2.

enter image description here

MWE

\documentclass[margin=2mm]{standalone}
\usepackage{tikz}

\begin{document}
\begin{tikzpicture}[scale=2]
\newcommand{\radioi}{1cm}
\newcommand{\radioii}{2cm}
\coordinate[label=below:$O$]  (O) at (   0:0       );
\coordinate[label=left:$A$]   (A) at (-135:\radioii);
\coordinate[label=right:$B$]  (B) at (- 45:\radioii);
\coordinate[label=right:$X$]  (X) at (  45:\radioi );
\coordinate[label=left:$Y$]   (Y) at ( 135:\radioi );

\draw (A) -- (B) -- (X) -- (Y) -- cycle;
\draw[dashed] (A) -- (X) (B) -- (Y);
\end{tikzpicture}
\end{document}
Sigur
  • 37,330
5

Conceptually the same as @Sigur's nice answer but with slightly different parametrization. There are two free parameters, which can be taken to be the length of the upper edge and the height. They go into commands of the sort

\draw[isosceleles trapezium=of width 2 and height 3 and name my trap];

This is illustrated in 

\documentclass[tikz,border=3.14mm]{standalone}
\begin{document}
\begin{tikzpicture}[isosceleles trapezium/.style args={of width #1 and height #2
and name #3}{insert path={
(45:{#1/sqrt(2)}) coordinate(#3-TR) -- (-45:{sqrt(#2*#2-#1*#1/2)}) coordinate(#3-BR) 
-- (-135:{sqrt(#2*#2-#1*#1/2)}) coordinate(#3-BL) -- (135:{#1/sqrt(2)}) coordinate(#3-TL) -- cycle}}]
\draw[isosceleles trapezium=of width 2 and height 3 and name my trap];
\draw[dashed] (my trap-TL) -- (my trap-BR) (my trap-TR) -- (my trap-BL);
\draw[latex-latex] ([yshift=2mm]my trap-TL) -- ([yshift=2mm]my trap-TR)
node[midway,fill=white] {$w$};
\draw[latex-latex] ([xshift=-2mm]my trap-TL -| my trap-BL) -- 
([xshift=-2mm]my trap-BL) node[midway,fill=white] {$h$};
\begin{scope}[xshift=6cm,rotate=30]
 \draw[isosceleles trapezium=of width 1 and height 2.5 and name another trap];
 \draw[dashed] (another trap-TL) -- (another trap-BR) (another trap-TR) -- (another trap-BL);
\end{scope}
\end{tikzpicture}
\end{document}

enter image description here

So the first parameter is w and the second one h. In addition, there is the name which is used to name the corners such that you can draw the diagonals, say. And of course you can rotate the thing and so on.

  • Very interesting. – Sigur Jan 10 '19 at 19:07
  • @Sigur I'll be happy to remove my answer. –  Jan 10 '19 at 19:21
  • Why? It is elegant and advanced for beginners. Good exercise to study the code. – Sigur Jan 10 '19 at 19:31
  • @Sigur Conceptually it is the same as your nice post. I slightly modified the parametrization to make my answer, which came later, not completely pointless. –  Jan 10 '19 at 19:58
  • You can define the polar command using as two arguments the length of semi-diagonals, as we did before. The computation is simpler and no tan and sqrt needed. Anyway, nice constructions. – Sigur Jan 10 '19 at 20:47
  • @Sigur I agree that it is simpler but I am not sure how the OP wishes to define the shape. Now they have two options: yours, which is more to the point, and mine in which TikZ takes care of all the nasty atan and sqrts. The OP never have to use sqrt or atan themselves if they go with my answer, but only specify the width and the height. –  Jan 10 '19 at 20:55
  • Good. I'll try to draw some arrows in my draw to show the lengths I used. – Sigur Jan 10 '19 at 20:56
4

A PSTricks solution just for fun purposes.

\documentclass[pstricks,12pt]{standalone}
\usepackage{pst-eucl}
\begin{document}
\foreach \a in {0,10,...,350}{%
\pspicture(-7,-7)(7,7)
    \pstGeonode(0,0){O}(2;\a){A}([offset=6]{A}O){B}
    \pstRotation[RotAngle=-90]{O}{A}[D]
    \pstRotation[RotAngle=90]{O}{B}[C]
    \psline(A)(B)(C)(D)(A)(C)(D)(B)
\endpspicture}
\end{document}

enter image description here

Algorithm

  • Define two points O and A.
  • Define point B such that OA is perpendicular to OB.
  • Define C as the image of rotating point B about O counter-clockwise.
  • Define D as the image of rotating point A about O clockwise.
  • Draw the lines.
Display Name
  • 46,933