You can use de the bodegraph package (https://www.ctan.org/pkg/bodegraph)
http://www.texample.net/tikz/examples/bode-plot/
for your example
first : the plot of the amplitude and phase diagrams
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}[xscale=15/4]
\begin{scope}[yscale=3/50]
\UnitedB
\semilog{0}{4}{-60}{60}
\BodeGraph[thick]{0:4}
{-\POAmp{1}{0.006}+
\SOAmp{1}{0.3}{100}}
\end{scope}
\begin{scope}[yshift=-7cm,yscale=3/90]
\UniteDegre
\OrdBode{15}
\semilog{0}{4}{-180}{90}
\BodeGraph[thick]{0:4}
{-\POArg{1}{0.006}+
\SOArg{1}{0.3}{100}}
\end{scope}
\end{tikzpicture}
\end{document}

second: with asymptotes
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}[xscale=15/4]
\begin{scope}[yscale=3/50]
\UnitedB
\semilog{0}{4}{-60}{60}
\BodeGraph[thick,red]{0:4}
{-\POAmpAsymp{1}{0.006}+
\SOAmpAsymp{1}{0.3}{100}}
\BodeGraph[thick]{0:4}
{-\POAmp{1}{0.0006}+
\SOAmp{1}{0.3}{100}}
\end{scope}
\begin{scope}[yshift=-7cm,yscale=3/90]
\UniteDegre
\OrdBode{15}
\semilog{0}{4}{-180}{90}
\BodeGraph[thick,red]{0:4}
{-\POArgAsymp{1}{0.006}+
\SOArgAsymp{1}{0.3}{100}}
\BodeGraph[thick]{0:4}
{-\POArg{1}{0.006}+
\SOArg{1}{0.3}{100}}
\end{scope}
\end{tikzpicture}
\end{document}

third : decomposing the transfer function
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}[xscale=15/4]
\begin{scope}[yscale=3/50]
\UnitedB
\semilog{0}{4}{-60}{60}
\BodeGraph[thick,red]{0:4}
{-\POAmp{1}{0.006}}
\BodeGraph[thick,green]{0:4}
{\SOAmp{1}{0.3}{100}}
\BodeGraph[thick]{0:4}
{-\POAmp{1}{0.006}+
\SOAmp{1}{0.3}{100}}
\end{scope}
\begin{scope}[yshift=-7cm,yscale=3/90]
\UniteDegre
\OrdBode{15}
\semilog{0}{4}{-180}{90}
\BodeGraph[thick]{0:4}
{-\POArg{1}{0.006}+
\SOArg{1}{0.3}{100}}
\BodeGraph[thick,red]{0:4}
{-\POArg{1}{0.006}}
\BodeGraph[thick,green]{0:4}
{\SOArg{1}{0.3}{100}}
\end{scope}
\end{tikzpicture}
\end{document}

You can also plot the Nichols plot with this package
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}
\begin{scope}[xscale=6/180,yscale=8/60]
\BlackGraph*[samples=150,black,smooth,ultra thick]
{-1:3.5}{-\POArg{1}{0.006}+
\SOArg{1}{0.3}{100},-\POAmp{1}{0.006}+
\SOAmp{1}{0.3}{100}}
{[right]{$H_2 $}}
\BlackGrid
\end{scope}
\end{tikzpicture}
\end{document}

with "l'abaque de Black-Nichols"
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}
\begin{scope}[xscale=6/180,yscale=8/60]
\BlackGraph*[samples=150,black,smooth,ultra thick]
{-1:3.5}{-\POArg{1}{0.006}+
\SOArg{1}{0.3}{100},-\POAmp{1}{0.006}+
\SOAmp{1}{0.3}{100}}
{[right]{$H_2 $}}
\AbaqueBlack
\StyleIsoM[blue,thick]
\IsoModule[2.3]
\BlackGrid
\end{scope}
\end{tikzpicture}
\end{document}

You can also plot the Nyquist plot
\documentclass{article}
\usepackage{tikz}
\usepackage{bodegraph}
\begin{document}
\begin{tikzpicture}
\begin{scope}[xscale=4,yscale=4]
\NyquistGraph[samples=150,black,smooth,ultra thick]
{-1:3.5}%
{-\POAmp{1}{0.006}+ \SOAmp{1}{0.3}{100}}%
{-\POArg{1}{0.006}+\SOArg{1}{0.3}{100}
}
\NyquistGrid
\end{scope}
\end{tikzpicture}
\end{document}

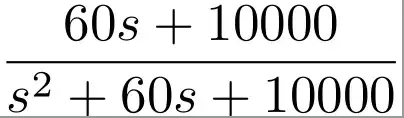
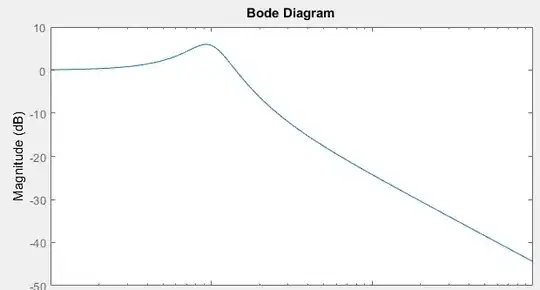








pgfplots? – Ktree Jan 07 '16 at 12:48