21

MWE:

\documentclass[12pt]{article}
\usepackage{amsmath}

\begin{document}
\thispagestyle{empty}

\[ \mathcal{F} \left\{ \sum_j e^{-2i\pi\nu_j t} \right\} \]

\end{document}

Result: sum in brackets

The sum only has a limit at the bottom, but the bracket size is calculated as if it had both limits, leading to a lot of unneeded space at the top. Is there a way to make the brackets wrap only the bottom limit?

cmhughes
  • 100,947
Krzysztof Kosiński
  • 342

5 Answers5

17

This is the expected behavior, as the braces are placed symmetrically with respect to the formula axis (running at the vertical center of the summation sign).

Use \Bigl\{ and \Bigr\} or, if too small, \biggl\{ and \biggr\} instead of \left\{ and \right\}:

\documentclass{article}
\begin{document}
\[
\mathcal{F}\Bigl\{\sum_{j}e^{-2i\pi\nu_j t}\Bigr\}
\]
\[
\mathcal{F}\biggl\{\sum_{j}e^{-2i\pi\nu_j t}\biggr\}
\]
\end{document}

enter image description here

egreg
  • 1,121,712
  • Seems like this is the only way that will not interfere with spacing from the surrounding text. – Krzysztof Kosiński Jul 13 '13 at 18:56
  • 2
    @KrzysztofKosiński The first, with \Big is the same as jhor's with \phantom, but takes into account the vertical space. Unfortunately, there are many shortcomings in \left and \right, which should be used with care. If you look closely, your formula has also an unwanted space between the F and the opening brace. – egreg Jul 13 '13 at 19:19
  • The extra space before brackets made by \left and \right can be removed by using the mleftright package. – Krzysztof Kosiński Jul 14 '13 at 00:37
11

You can vertically center the sum this way:

\documentclass[12pt]{article}
\usepackage{amsmath}
\newcommand*{\mvcenter}[1]{\vcenter{\hbox{$\displaystyle #1$}}}
\begin{document}
\thispagestyle{empty}
\[
  \mathcal{F} \left\{ \mvcenter{\sum_j e^{-2i\pi\nu_j t}} \right\}
\]
\end{document}

Image of output

I would use it with care: you have symmetry now, but the inner formula baseline is different then.

Stefan Kottwitz
  • 231,401
6

Two other solutions, which IMO are neither better nor worse in the technical point of view, is the combination of \smash and \vphantom, or the \textsyle typesetting :

\[ 
\mathcal{F} \left\{ \vphantom{\sum}\smash{\sum_{j}} e^{-2i\pi\nu_j t} \right\}
\quad\text{or}\quad
\mathcal{F}\Big\{ \textstyle\sum_{j} e^{-2i\pi\nu_j t}\Big\}
\]

where the base line of \mathcal{F} remains the same as that of the \Sigma. enter image description here
EDIT : If you are not happy with this, you can put j on the line by using \sum\nolimits_{j}.

For further fine tuning of the delimiter height and of the equation height, you can load the calc package and define the macro :

\newlength{\hhh}
\newcommand{\mstrut}[2][2]{%
\settototalheight{\hhh}{$\displaystyle #2$}%
\rule[-0.5\hhh*\real{#1}+0.5ex]{0pt}{#1\hhh}%
}

drawing an invisible rule the height of which is the one of the mandatory argument multiplied by optional one (set to 1 by default). With this macro, and the code

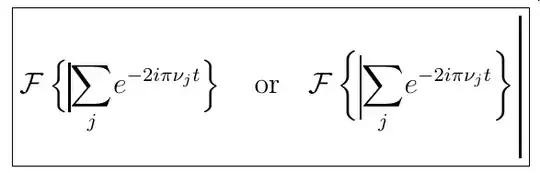
\[ \boxed{
  \mathcal{F} \left\{\mstrut[0.7]{\sum_{j}} \smash{\sum_{j}} e^{-2i\pi\nu_j t} \right\} 
  \quad\text{or}\quad
  \mathcal{F} \left\{\mstrut[0.9]{\sum_{j}} \smash{\sum_{j}} e^{-2i\pi\nu_j t} \right\} 
  \mstrut[2]{\sum_{j}}
} \]

we get:
enter image description here EDIT : suppressed the \vphantum in the above code, because it's super seeded by the \mstrut.

where the \mstrut thickness is set to 1pt for demonstration purpose, and the box materialize the upper and lower limits of the equation.

By this way, choosing the proper value int \mstrut[?]{} you control both the size of te delimiters and the verical spacing...

Jhor
  • 4,179
  • I like the first solution with \vphantom, but it seems that the displayed equation now has too little spacing from the text below it. Using vspace doesn't seem to work, because it looks like it adds an empty paragraph below the equation. Is there a way to add a little bit of space at the bottom? – Krzysztof Kosiński Jul 13 '13 at 18:52
  • I explain in the EDIT how two fine tune everything – Jhor Jul 13 '13 at 20:43
2
\documentclass{article}
\usepackage[utf8]{inputenc}
\begin{document}

\begin{equation}
\mathcal{F} \left\{\sum_{j}\nolimits e^{j^{\exp 2}+i\det U - 1}\right\} = 0
\end{equation}

\end{document}

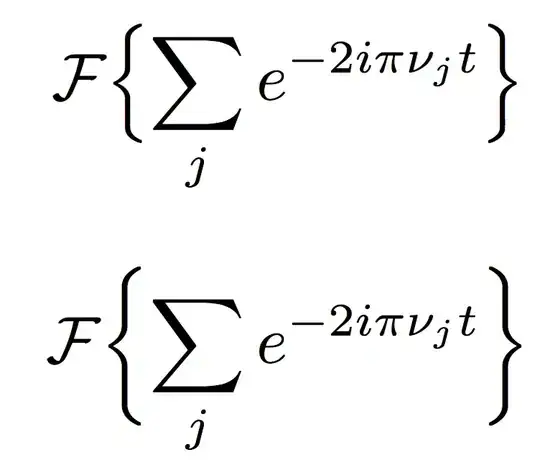
enter image description here

It just makes the indices not-exactly-limits as in they are not at top and at the bottom but instead at the corner, so that the fourier transform only knows about the sigma, not the indices.

2

You may also use \raise or \lower command to move the brackets.:

 \[ \mathcal{F} {\lower4.5pt\hbox{$\bigg\{$}} \sum_j e^{-2i\pi\nu_j t} {\lower4.5pt\hbox{$\bigg\}$}} \]

Thus the brackets contains their arguments without too much space above, but now you have not a symmetric formula: if you add a set operator after \mathcal{F}, it will be aligned with this glyph, not with the centre of the bracker.

Martino
  • 1,400