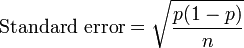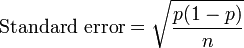I am attempting to calculate the standard error (SE) for the positive predictive value (PPV), negative predictive value (NPV), and diagnostic odds ratio (DOR) that I have obtained using the rates of true positives, false positives, true negatives, and false negatives in a sample. I am able to get 95% CIs but not SE.
Thank you!
The PPV and NPV are proportions. You know the numerator and denominator, which both are positive integers, so you can calculate the proportion. Your goal, I presume, is to quantify how well you have determined those values. If your sample size is huge, then those values are likely to be very close to their true population values. If the sample size is small, then there is more random variability and those values are more likely to be far from their true value.
The confidence intervals you calculated tell you what you want to know. Given a bunch of assumptions, you can be 95% confident that the confidence interval includes the population value.
What about the standard error? The problem is that the uncertainty of a proportion is not symmetrical. The asymmetry is very noticeable when the proportion is far from 0.50 and the sample size is small. Since the confidence interval is not symmetrical around the observed proportion, trying to express this uncertainty as a single plus/minus standard error won't be very informative. It makes more sense to report the confidence interval.
If you really want to calculate a standard error, even knowing it isn't very helpful, here is the formula to compute an approximate standard error from p (the proportion) and n (sample size; the denominator):
As an addition to Harvey's response if you have a small sample of data then there are alternatives to the standard error approximation formula shown above. I would recommend using software, one example would be to use the binom.test function in R, to calculate these confidence intervals rather than doing it "by hand".
