Logistic regression diagnostics when predictors all have skewed distributions

Question

I'm fitting a logistic regression model Y ~ X1...X10 to 10,000 observations, where my goal is estimate the effect of each covariate on Y.

My first issue is deciding what transformations to apply to the predictors. They all have very skewed distributions, and in some cases take on very few (<6) values. I included a typical histogram below. Would it make sense to cast them as factors, or otherwise apply some power transformation?

I'm having some trouble diagnosing the model. The fit is quite poor - the classification rate is only 65%, and the deviance is:

Null deviance: 13568  on 9999  degrees of freedom
Residual deviance: 13143  on 9989  degrees of freedom

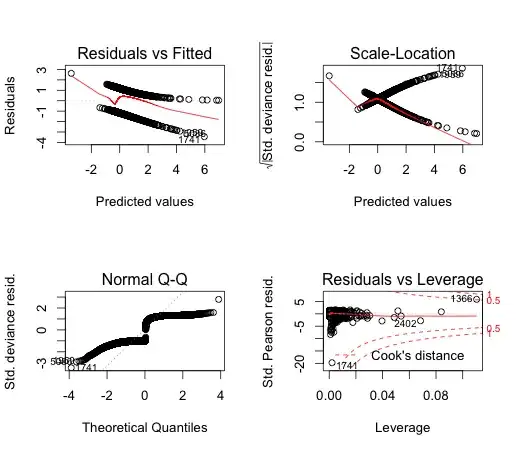
The diagnostic plots shown below seem to suggest:

1. There are some very high leverage, high residual points affecting the fit of the model. I think these the points in the tails of the distributions, which don't represent the rest of the data. Would transforming the data solve this problem?
2. There residuals are definitely not normally distributed. There is a trend the model fails to capture. How should I find this trend?
3. The deviance residuals are definitely not normally distributed.

I guess my main question is how to find a suitable transformation of the data, and the best next step to explaining the remaining variance in the data.

Answer 1

The distribution of the predictors is almost irrelevant in regression, as you are conditioning on their values. Changing to factors is not needed unless there are very few unique values and some of them are not well populated.

But with very skewed predictors the model may fit better upon a transformation. I tend to use $\sqrt{}$ and $x^{\frac{1}{3}}$ because these allow zeros, unlike $\log(x)$. Then when the sample size allows I expand the transformed variables in a regression split to make them fit adequately, e.g.

require(rms)
cuber <- function(x) x^(1/3)
f <- lrm(y ~ rcs(cuber(x1), 4) + rcs(cuber(x2), 4) + rcs(x3, 5) + sex)

rcs means "restricted cubic spline" (natural spline) and the number after the variable or transformed variable is the number of knots (two more than the number of nonlinear terms in the spline). When you make the distribution more symmetric (here with cube root), it frequently requires fewer knots to get a good fit.

AIC can help in choosing the number of knots $k$ if you force all variables to have the same number of knots. Below, $k=0$ is the same as linearity after initial transformation.

for(k in c(0, 3:7)) {
  f <- lrm(y ~ rcs(cuber(x1),k) + rcs(cuber(x2),k) + rcs(x3, k) + sex)
  print(AIC(f))
}