1

I have a large dataset (n > 500,000) which I'm building a linear model with lm(PV1READ ~ PV1MATH + PV1SCIE + ST004D01T). Tests for Normality, No multicollinearity, Independence seem fine, but it keeps tripping up on Homoscedasticity. The Breusch-Pagan test ols_test_breusch_pagan(mdl) gives:

Chi2 = 930.8976, Prob > Chi2 = 1.88444e-204

I read elsewhere that B-P tests aren't so good on larger datasets (p values go down the more observations I add), but the White's test gives similar results white_test_boot(mdl):

Test Statistic: 1053.69, P-value: 0

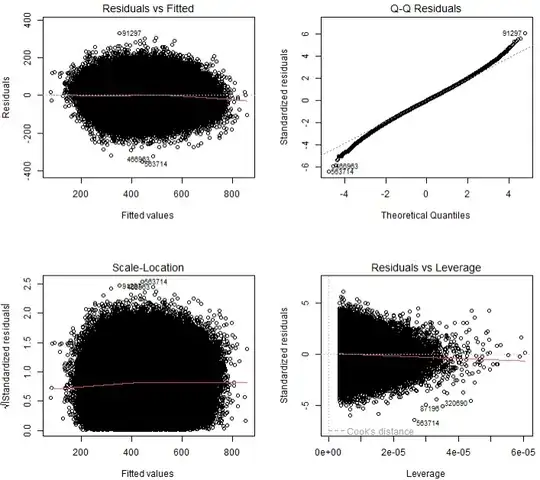
I would just kick the model out, but the plots look promising, the lines are pretty straight to me:

enter image description here

But when I plot the Studentized Residuals, a large number of points are |Residual| > 2

enter image description here

sum(abs(stud_resids)>2)/ length(stud_resids)

Which equates to ~5% overall, which seem ok.

Am I missing something? Can I just use the graphs instead of the tests if the dataset is large enough? And how would I report that?

Durden
  • 1,171
pluke
  • 159
  • 6
  • 1
    I believe that proposed duplicate addresses this. If not, please say what remains unclear, and we can talk through it in the comments, or I can reopen the question to allow for a full answer. – Dave Mar 19 '24 at 17:48
  • 2
    Like all Lagrange-multiplier (LM) tests, the Breusch-Pagan test can be written as $n R^2$, where $n$ is your sample size and the $R^2$ is that of the auxiliary regression of the squared residuals of your model on $x_1, x_2, x_3, \ldots, x_k$. For a large enough $n$, this test will always reject. Which is to say: trust your eyes, and your common sense. – Durden Mar 19 '24 at 18:19
  • Thanks @Durden, does the same problem exist with whites test? – pluke Mar 19 '24 at 19:59
  • 1
    White's test is also an LM test, so the same logic applies. – Durden Mar 19 '24 at 20:18
  • 1
    Bottom line: when your sample size is in the hundreds of thousands, these tests will exceed usual "critical values" for the tiniest deviations from pure homoscedasticity; deviations that aren't meaningful enough warrant an adjustment of your model. – Durden Mar 19 '24 at 20:33

0 Answers0