Why do we maximize likelihood (sum of logs) and not simply maximize sum of probabilities?

Question

In logistic regression we find the maximum likelihood estimator - $\max \prod_{i} p(y_i \mid x_i)$. Which in practice means maximizing the sum of log likelihoods. This makes sense, I understand MLE.

But... what is wrong with simply maximizing the likelihoods? In other words, if our model is a simple logistic regression on some dataset $(x_i\in \mathbb{R}^d,y_i \in \{-1,1\})$, I am asking about the difference between the following two optimization problems (with and without log):

$$\max_{W} \sum_{i : y_i = 1} \log \left(\frac{1}{1+\exp(-W^Tx_i)}\right) + \sum_{i : y_i = -1} \log \left(1 - \frac{1}{1+\exp(-W^Tx_i)}\right)$$

$$\max_{W} \sum_{i : y_i = 1} \left(\frac{1}{1+\exp(-W^Tx_i)}\right) + \sum_{i : y_i = -1} \left(1 - \frac{1}{1+\exp(-W^Tx_i)}\right)$$

I wrote some simple code for training a 2 parameter model (slope and intercept) with gradient descent and both methods work... except for two things:

• The first has a nicer loss curve, seems less sensitive to initialization, trains faster, etc.
• I know that nobody actually does the second

Could someone give both an intuitive explanation and a mathematical one? I have read various blog posts about "scoring rules" (e.g., https://yaroslavvb.blogspot.com/2007/06/log-loss-or-hinge-loss.html), but I still don't get it. What properties does log have in this context that make it better behaved? I understand all the connections between the log loss to cross entropy, MLE, etc.; what I don't understand is why the second option (no log) is bad. In a practical sense I have some vague intuition about log stretching the range of the loss from $[0,1]$ to $[-\infty, 0]$. I also have some intuition that accuracy (or error) should be thought of on a log scale because going from 80% to 90% accuracy is the same relative improvement as 90% to 95%. Anyways, sorry for rambling - I would like to have some stronger intuition and some formal math/stats to back this.

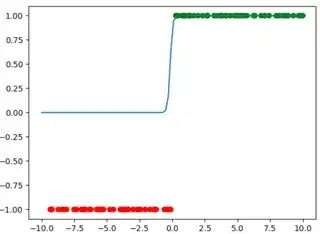
Here is the loss curve for the second (no log) optimization on some very simple separable data. Notice how long it gets stuck in a local minima. The other optimization finishes in very few steps. On the right is the data and output logistic model.

EDIT: It seems something similar has been asked before in different words but that question seems to ask about $p(x_i \mid W)$, meaning generative modeling not classification. The top answer is about how sum of probabilities corresponds to "at least one event is true" instead of "all events are true" but that doesn't seem to apply in my case. If nothing else, the global minima of both loss functions (with/without log) both correspond to perfect classification.

Also, one of the comments says "I don't like this kind of post, MLE is statistically justified, the sum of likelihoods is not". That's fair, but my goal here is to figure out how to explain things to a beginner. I just told them about linear regression and I would to be able to explain to them why one "obvious thing" in classification is bad, which is simply to express what you want as a loss (train a model of $p(y=1\mid x)$ to output high probability for positive labels and low probability for negative labels).

Answer 1

There are two issue here. First, on philosophical grounds, there is an argument that for some reasonable definitions of evidence, the likelihood contains all the evidence in the sample. That's very clearly true for the case of choosing between two precise hypotheses, where we can prove that the best test uses the likelihood ratio.

Second, the problem with sums of probabilities is that the difference between small and very small gets neglected. At the extreme, if a particular set of parameter values would make the likelihood equal to zero, we can rule out that set of parameter values; it's impossible. If you used the sum of the probabilities for inference, you wouldn't rule out parameter values than made a single probability equal to zero. The difference between 0 and 0.001 would be much less important than the difference between 0.5 and 0.49.

As a result of both issues, the esimator maximising the sum of the probabilities won't be as good as the sum of the logs, even in situations where exactly-zero probabilities aren't an issue. For example, suppose we want to estimate $\mu$ in 100 observations from $N(\mu,1)$. The MLE is unbiased, approximately Normal, and has standard error 0.1. The maximum-sum-of-probabilities estimator, based on a small simulation, is also unbiased and approximately Normal, but has standard error approximately 0.125.

Outlying observations, which have large influence on the MLE in this problem, will have small influence on the sum-of-probabilities estimator, which I suspect is why its efficiency is relatively low. It still does better than I'd expect in this problem.

In problems with less symmetry the sum-of-probabilities estimator need not even be consistent. Consider, for example, Bernoulli(p) observations. The probability is $p$ or $1-p$ and the sum of probabilities $$S(p)= (\sum Y_i) p + (\sum 1-Y_i)(1-p)$$ the derivative with respect to $p$ is $$S'(p)= (\sum Y_i) - (\sum 1-Y_i)$$ which does not depend on $p$. The maximum of $S(p)$ occurs at $p=0$ if the mean of $Y$ is less than 1/2 and at $p=1$ if the mean of $Y$ is greater than 1/2. This is a terrible estimator: it's not consistent, but even worse, $p=0$ and $p=1$ are impossible values for $p$ unless all the $Y$ are zero or all the $Y$ are 1.

So: no.

Answer 2

The simple reason is that if probabilities are in a chain, for example, for it to snow, one needs both precipitation and low enough temperature, thus the probability of snow ($p_s$) is the probability of precipitation ($p_p$) TIMES the probability of low enough temperature ($p_t$), or $p_s=p_p\cdot p_t$. Now logarithms transform multiplication into addition such that we can write $\ln p_s=\ln p_p+\ln p_t$. So we have transformed a product rule into a sum rule. Then, since we have a sum rule, we can find a maximum using least squares regularization, or L$_1$ optimization or whatever. Thus, transforming back into the original equation, we have found the maximum probability product of $p_s=p_p\cdot p_t$.

However, this is not the case for $p_?=p_p+ p_t$. If we maximize that sum, we will have maximized $p_?$, where $p_?$ is a sum of probabilities, but is not directly related to probabilities that follow a chain rule, i.e, conditional probabilities that say "How much of this times that times whatever..." So, one might produce answers that set $p_p=0$ and $p_t=\text{Max possible}$ or some such, but one would have to have a very special circumstance for that to have meaning.

As I say below in a comment "Perhaps showing the log loss for logistic regression is what you are seeking?"