The data structure looks fine except Day needs recoding. I guess Day = 1 for Treatment = Before and Treatment = After are different days. Assuming Day = 5 when Treatment = Before is the last day before treatment, we can redefine Day = ifelse(Treatment == "Before", Day - 5, Day) so that Day ranges -4 to 5.
Björn gave the Bayesian approach. In frequentist mixed-effects modeling, there are also options to incorporate error-variance heterogeneity. Using nlme, a model could be
lme(Y ~ Treatment * Day + X1 + X2, random = ~ 1 | Subject, weights = varIdent(form = ~ 1 | Treatment))
gls(Y ~ Treatment * Day + X1 + X2, correlation = corAR1(form = ~ Day | Subject), weights = varIdent(form = ~ 1 | Treatment))
Random slopes of Day before and after treatment by Subject are worth testing. The random-intercept model is equivalent to GLS with a compound-symmetry correlation structure where correlation = corCompSymm(form = ~ 1 | Subject).
glmmTMB also estimate heteroscedasticity with random effects and correlated errors. See tutorials https://cran.r-project.org/web/packages/glmmTMB/vignettes/covstruct.html.
glmmTMB(Y ~ Treatment * Day + X1 + X2 + (1 | Subject), dispformula = ~ Treatment, family = gaussian)
glmmTMB(Y ~ Treatment * Day + X1 + X2 + ar1(0 + factor(Day) | Subject), dispformula = ~ Treatment, family = gaussian)
See a tutorial https://hbiostat.org/rmsc/long that includes both frequentist and Bayesian longitudinal data analysis.
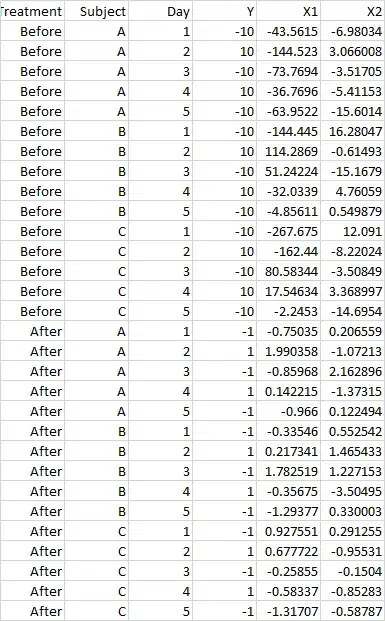
dput(<yourData>)to your question is easiest. Also explain what situation your toy data is suppose to represent. For example, what does it mean that patient A has a before measurement and after measurement on days 1, ..., 5? – dipetkov Feb 22 '24 at 10:40