1

I am working on a time-series forecasting problem with ARIMA. Since long-term predictions were not good, I've started using a "rolling ARIMA" like explained here

for t in range(len(test)):
 model = ARIMA(history, order=(5,1,0))
 model_fit = model.fit()
 output = model_fit.forecast()
 yhat = output[0]
 predictions.append(yhat)
 obs = test[t]
 history.append(obs)

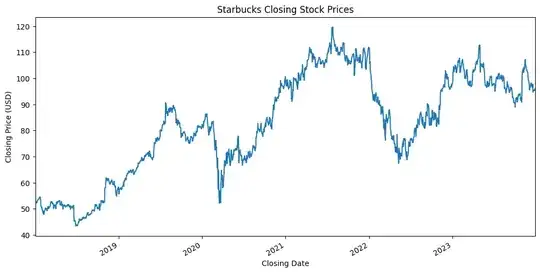
My data looks like this:

bitcoin prices sbux prices

ADF test says they are not-stationary, but after differencing once the test says they are stationary.

I run a gridsearch over the ARIMA orders p,q,d on values 0,1,2 for all three of them, and measure the MAPE and MSE. I used the non-differenced data, because I will anyway include a d=1,2 in the process, to get the different performances.

The best model turns out to be an ARIMA(0,1,0), which is basically using a random walk at each step.

Does this result make any sense? I would expect to have AR and MA terms.

Richard Hardy
  • 67,272
nico_so
  • 83
  • As the answers indicate, an ARIMA(0,1,0) absolutely makes sense for financial data. However, simple methods like the random walk are also often surprisingly effective in other applications, e.g., here and here (which also has an element of "I would have expected some dynamics"). – Stephan Kolassa Jan 07 '24 at 18:11

2 Answers2

4

Yes, it makes sense. It is in line with the common observation that the best prediction of an asset's price is its last observed value plus a constant that accounts for the risk of holding an asset with an uncertain future price. If there were AR or MA terms that made the price predictable, investors would find this out, apply the ARIMA model and buy the asset before it appreciates or sell before it depreciates. Their buying/selling would change the supply/demand balance and thus raise/lower the price of the asset immediately. Once that has happened (and that happens very quickly with algorithmic trading), the expected change in price would again be just the constant reflecting the risk.

Richard Hardy
  • 67,272
2

I think $ARIMA(0,1,0)$ make sense. You are challenging to most hard to predict. In the first figure, one can say that there is a trend only, $d=1$. AR or MA terms, especially p,q,d on 0,1,2 couldn't explain bitcoin data, because that statistcal model is too much simple. From mathematical background, a significant term of AR 1 means a future data $y_{t+1}$ can be predicted by $y_{t}$, more easily, p,q,d on 0,1,2 is same to say "I want to next day's bitcoin price from today and yesterday only". I don't think so.

ps. In many case of financial data is assumed as gBM(geometric Brownian Motion), which is more easier to handle with log transformed. As you know, your data is non-stationary but it's not only up to constant mean. Variance is also important for many statistical tools.

Ryu Dae Sick
  • 95