Interpretation of Maximum Likelihood Value

Question

I have a question about Maximum Likelihood values, and how to interpret them.

In order to explain the question, please see the Figure below. I will add explanation for how this figure has been created at the end of this question.

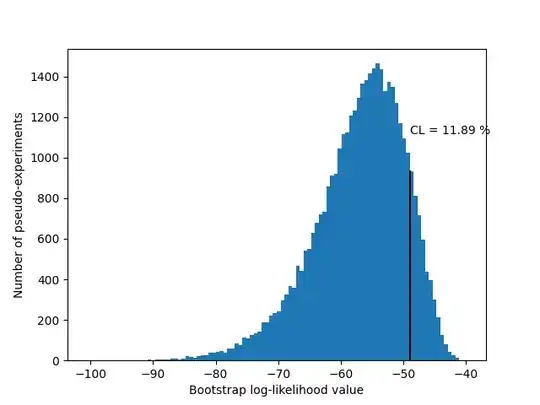
From the figure it can be see that the value obtained from the Maximum Likelihood Estimation between model and data was approximatly -49, as shown by the black line. This is a log-likelihood value obtained from a MLE between data and model.

The rest of the entries in the histogram are obtained from a bootstrap procedure, where the data was randomly sampled with replacement.

The Confidence Level (which I may have calculated the wrong way round to as would be traditional) is approximatly 12 %. This means that approximatly 12 % of the pseudo-experiments returned better fits, and 88 % returned worse fits.

My question is, now that I have obtained this figure, how should I interpret it?

It is unlikely that a random bootstrap sample provides a better fit between model and data. Approximatly 9/10 random bootstrap samples produce a worse fit between model and data, because the LL value is more negative in these cases.

Beyond that, I don't know what can be interpreted from this. This figure doesn't seem to express much in the way of a "good" vs "poor" fit. It might be that I just don't fully understand how to draw such a conclusion.

If this set of data is better than 90 % (ish) of random bootstrap samples, that seems to suggest the fit might be quite good?

I do not yet have plots of the distribution of model parameters. Perhaps the fact that I am missing these figures is partly why I cannot draw much in conclusion from this figure alone?

Figure Explanation:

The above figure shows a distribution of Likelihood Values generated in a numerical experiment. (Actually they are log-likelihood values but it is easy to convert between the two.)

The black line represents the result of a Maximum Likelihood estimation between a set of data and a model function. The log-likelihood value obtained was approximatly -49.

The remainder of the data in the histogram were obtained by creating a bootstrap sample from the data, and performing the MLE procedure repeatedly, measuring the obtained LL value each time. There are about 40,000 numerical experiments represented in the histogram in the figure.

Answer 1

This is not a complete answer, but two possible initial aveneues for an answer.

There are two key concepts which I think are worth considering.

• Each LL value is obtained by re-sampling the original data. So by re-sampling the data we are able to obtain LL values which occur more often, as well as values which occur less often

• The peak of the distribution gives the most probable value

While the LL value itself is arbitrary (we can add any constant to our LL value and obtain the same distribution of results, shifted by a constant) the distribution is meaningful, in particular making a comparison between the LL value obtained from data and the distribution obtained from bootstrap re-sampling is meaningful.

• If our observed data LL value lives inside a bin with small probability, then almost any possible re-sampling of the data will produce a more frequently occuring LL value.
• If our observed data LL value lives at the peak of the distribution, then almost no re-sampling produces a more probable value.

Since the bootstrap samples themselves are generated from the data I am not sure exactly how significant the above two statements are.

One possible consideration might be that if our data contains a small number of outliers which distort the LL value, then we might expect a re-sampling to remove those values, and therefore on average with high probability we will frequently obtain a bootstrap sample with smaller negative LL value. (Better fit to data.)

This could be tested with some simple MC, and I will try to test it soon.

Answer 2

I can reproduce this when I consider (for example) a model with Gaussian noise. Then the loglikelihood can be expressed very easily; namely in terms of the sum of squared residuals $ \sum_{i=1}^n r_i^2$

$$\text{logLik} = - \frac{n}{2} \log\left( \frac{2\pi e}{n} \sum_{i=1}^n r_i^2 \right) $$

When you resample the observations $y_i$, then you may randomly get a sample with smaller variance such that the residuals (which are related) will be also smaller and the loglikelihood higher.

Only if you have a strong fit, then this resampling will generate consistently larger residuals with high probability. However, if the $R^2$ is not high then resampling may generate small values as well.

Below is a computation of the above situation also added is an approximation for the distribution of the loglikelihood with estimates of the mean and variance of $\sum r_i^2$ based on the mean and variance of the observed values $y_i^2$ with a correction of $(n-2)/n$ since fitting will make residuals smaller than the variance in the sample. Also we use the approximation for the logarithm as described here: If $X$ is normally distributed, can $\log(X)$ also be normally distributed?

The red line is the likelihood of the fitted model, the histogram are likelihoods obtained with resampled data, the green line is an estimate for the distribution of the likelihoods of the resampled data.

n = 100     # data points
m = 10000  # simulations
set.seed(1)
x = rnorm(n)
y = 0.5*x+rnorm(n) # data
model of a line
and it's likelihood and slope coefficient
mod = lm(y~1+x)
ll_mod = logLik(mod)
slope_mod = mod$coef[2]
repeat with resampled data
ll = c()
slope = c()
for (i in 1:m) {
    sel = sample(1:n,n,replace = TRUE) 
    sel2 = sample(1:n,n,replace = TRUE) 
    mod_sample = lm(y[sel]~1+x[sel2])
    #mod_sample = lm(y[sel]~1+x[sel]) ### paired resampling (creates a much different graph)
    ll = c(ll,logLik(mod_sample))
    slope = c(slope,mod_sample$coef[2])
}
hist(ll, xlim = c(-180,-120), breaks = 20, freq = 0)
lines(c(1,1)*ll_mod,c(0,m), col = 2, lwd =2)
approximation
mean and variance of the squared sample valued
m = mean(y^2)
v = var(y^2)
expected mean and variance of sum of squared residuals based on the sample
ms = 2piexp(1)m(n-2)/n
vs = (2piexp(1))^2v/n((n-2)/n)^2
mean and variance after multiplications and taking the log
ml = (log(ms) - 0.5 * vs/ms^2)(-n/2)
vl = (vs/ms^2)(n/2)^2
plot line
lls = seq(-200,-60,1)
lines(lls,dnorm(lls,ml,vl^0.5), col = 3)

It becomes easier to see when we plot the histogram of a function of the log likelihood

$$ \frac{2}{n \pi e} \exp\left(-\frac{2}{n}\text{logLik} \right) = \sum_{i=1}^n r_i^2$$

Then the approximation is more accurate (no logarithm involved) and the distribution is easier to interpretate.

The distribution of the sum of squared residuals in resampled simulations relates to the variance of the original $y_i$. The mean will be $\mu_{RSS} \approx (n-2) \text{Var}(y_i)$ and (for normal distributed $y_i$) the standard deviation will be $\sigma_{RSS} \approx \sqrt{2} \mu$. In comparison, the red line will be at $n (1-R^2) \text{Var}(y_i)$ and the distance between the red line and the mean of the histogram in terms of standard deviations is approximately $R^2/\sqrt{2}$.

hist(exp(ll*-2/n)*n/2/pi/exp(1), xlim = c(50,200), breaks = 20, freq = 0)
lines(c(1,1)*exp(ll_mod*-2/n)*n/2/pi/exp(1),c(0,m), col = 2, lwd =2)
lls = seq(50,200,1)
lines(lls,dnorm(lls,m(n-2),sqrt(v(n-2)^2/n)), col = 3, lwd = 2)

Answer 3

I had some further thoughts which don't quite fit into the previous comments I posted.

Firstly, to present some results from an experiment. In the attached figure there are 11 histograms. They should be viewed as going from "right to left". Each histogram color is for a different experiment. The experiments differ by the number of outlier values added to the data.

To explain in further detail:

• The rightmost histogram is generated from data with no outliers.
• 100 values are drawn from a Gaussian distribution with a mean of 0 and a standard deviation of 1.
• A Gaussian model is fit to the data using the method of maximum (log) likelihood. There are two variable parameters, the mean and standard deviation. The log-likelihood value is saved
• 10,000 bootstrap samples are generated from this data
• For each bootstrap sample the process is repeated
• A histogram of the resulting log-likelihood values is produced
• This histogram is shown in dark blue tab:blue, it is the rightmost histogram

It occured to me that in this re-sampling process, we would not expect anything special to happen. All of the original dataset are values drawn from a Normal distribution. If we resample this, we obtain another dataset which consists entirely of Normally distributed values. It produces, statistical speaking, the same result as if we had just drawn 100 new samples from a Normal distribution with the same parameters as before.

The resulting histogram of log-likelihood values appears to be Gaussian itself, and this is perhaps not surprising.

For other histograms in the figure below, outliers are introduced. The orange dataset contains 1 outlier, with 99 values drawn from the same distribution as before.

• Outliers are generated by drawing from another Gaussian distribution with the same mean ($\mu=0$), but with 10x larger standard deviation ($\sigma=10$).

The next line, green, contains 2 outliers. Each histogram moving to the left contains 1 more outlier than the dataset to its right. The blue histogram which peaks furthest to the left is generated from a dataset containing 10 outliers.

Quite why the data looks the way it does I am not totaly sure. But I wanted to present these results. It would be interesting to repeat this experiment with more outliers, eventually having number of outliers = 100, entirely replaing the original dataset.

Update:

I performed the above experiment and obtained these results.

Another Update:

I ran another simulation overnight and obtained this result.

This is two sets of bootstrap samples, one with no outliers and one with a single outlier drawn from the same distribution (Gaussian) with the same mean (0) and a stddev 10x larger. (10)

To really interpret thsi properly I think I need to so more investigation into the data value, which here is -135.7.

Here's the same figure for number of outliers = 2.

And number of outliers = 5.

Answer 4

I've had yet further thoughts about this which again don't really fit into any of the previous answers I have posted, so here goes...

I began thinking about this problem at a much more basic level.

• To make any further conclusions about the LL values and distributions observed, we should first be able to make some conclusions from an ideal situation
• That would be: A set of data drawn from a known distribution with no outliers
• If we had such an idealized situation perhaps we could make some conclusions by comparing a LL distribution in the ideal world compared to a distribution we actually observed in some real world experiment

To make it concrete, let's do some numerical experiment with Gaussians.

We want to know something like if we draw a certain number of samples from a Gaussian and fit a Gaussian model to it using the method of Maximum Likelihood, then what is the distribution of log-likelihood values obtained?

Then further - can we say anything about these values from theory?

Let's begin with two figures.

• The underlying model is a Gaussian with $\mu=0, \sigma=1$
• We draw $n$ samples from this distribution
• Each histogram color is for a different value of $n$
• The value of $n$ used are 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 for the first figure, and 2, 3, 4, 5, 6, 7, 8, 9, 10 for the second figure.
• The value 1 is special, we shall say more about it later
• For each experimental run, we have a chosen value of $n$. We draw $n$ samples and then obtain a measurement of the log-likelihood value via the method of Maximum Likelihood
• This process is repeated $10000$ times. That is to say, each histogram contains $10000$ entries

A few conclusions:

• From the first figure, it appears that the expected LL value is approximatly a linear function of the number of samples drawn ($n$)
• From the second figure we note it is possible to obtain LL values greater than zero, but that these are highly improbable even for relatively small values of $n$

Let's perform a linear fit between $n$ and the LL value. The residuals for that look like this:

• We can see it is not quite linear
• The errorbars drawn are obtained from the standard deviation of each LL distribution
• Despite the large error, the variance between each of the points is low and we can clearly conclude a non-linear model is required to obtain a good fit to the data

I can't say anything further about that at this point.

---

Theoretical Considerations

The special value $n=1$ might guide us towards something. We note that for $n=1$ we do not have any sensible value for the Gaussian parameter $\sigma$. However, we know that the likelihood is maximized by choosing an arbitrary value for $\sigma$ and setting $\mu$ equal to the single value drawn from the distribution. Given that our model has the form of a Gaussian $$p(x_i;\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2}\left(\frac{x_i-\mu}{\sigma}\right)^2\right)$$ we can say that the Maximum Likelihood is obtained by setting $x_1=\mu$, and therefore the likelihood value obtained is $$\frac{1}{\sqrt{2\pi\sigma^2}}.$$

Note that this is not the log-likelihood, but likelihood, which is being considered here. We can convert between them.

From this we might conclude that on average we will obtain values with some variance and that the size of this variance might tell us something about how spread out the datapoints are and therefore what the expected value of our likelihood function might be for larger values of $n$.

• I attempted to calculate it for $n=2$, but I need more time to check my results on this. I think the calculation is fairly simple to do.