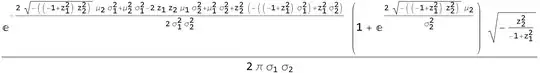Formulas, approximations, or bounds for $\mathbb{E}\left( \frac{X}{\lVert X \rVert} \right)$, $X\sim N(\mu, \Sigma)$?

Question

In another question, I asked for $\mathbb{E}\left( \frac{X}{\lVert X \rVert} \right)$, in the case where $X \in \mathbb{R}^d \sim N(\mu, I_{d})$. Somebody posted an exact formula based on the symmetry of the isotropic covariance case.

I am now interested in obtaining some expression (or approximation) for the more general case where $X \sim N(\mu, \Sigma)$ and $\Sigma$ is any diagonal matrix.

As I mentioned in this related question, one possible approximation involves using a Taylor approximation, in which: $\mathbb{E}\left( \frac{A}{B} \right) \approx \frac{\mathbb{E}(A)}{\mathbb{E}(B)} - \frac{Cov(A,B)}{\mathbb{E}(B)^2} + \frac{\mathbb{E}(A)var(B)}{\mathbb{E}(B)^3}$, where I would have $A = X$ and $B = ||X||$ in the description above. For using this approximation, however, I'm not sure about the required $\mathbb{E}\left( ||X|| \right)$, $Var \left( ||X|| \right)$ and $Cov(X, ||X||)$ (the first two are related to the non-central chi distribution which has known moments, but I'm not sure I can use this distribution since each $X_i$ has a different variance).

So, I'm wondering whether there is some other reasonable way to approximate $\mathbb{E}\left( \frac{X}{\lVert X \rVert} \right)$, or whether the missing pieces in the approach I propose above can be obtained.

Of note, the random variable $\frac{X}{||X||}$ with $X \sim N(\mu, \Sigma)$ and any $\Sigma$ is the general projected normal distribution.

Edit: The approach proposed in the comments of using Cauchy-Schwarz inequality could be useful. For that, we'd need $\mathbb{E}\left(\frac{1}{||X||^2}\right)$ which is a challenging problem (see here, here).

Answer 1

Following one of the comments, we can approximate $\mathrm{E}\left( \frac{X}{||X||} \right)$ with $X \sim \mathcal{N}(\mu, \Sigma)$ by using a second-order Taylor series.

Each element $i$ of the vector $\mathrm{E}\left( \frac{X}{||X||} \right)$ is given by $\mathrm{E}\left( \frac{X_i}{||X||} \right)$. Thus, we can solve the problem by finding the expected value of $f(u,v) = \frac{u}{\sqrt{u^2+v}}$, where $u=X_i$ and $v=\sum_{i=1 }^{i=n} X_j^2 - X_i^2= \sum_{j \neq i} X_j^2$.

The Taylor approximation for $\mathrm{E}(f(u,v))$ has general form:

$$\mathrm{E}(f(u,v)) \approx f(\hat{u},\hat{v}) + \frac{1}{2}\frac{\partial^2 f}{\partial u^2}\bigg|_{\substack{u=\hat{u}\\v=\hat{v}}} Var(u) + \frac{1}{2}\frac{\partial^2 f}{\partial v^2}\bigg|_{\substack{u=\hat{u}\\v=\hat{v}}} Var(v) + \frac{1}{2}\frac{\partial^2 f}{\partial u \partial v}\bigg|_{\substack{u=\hat{u}\\v=\hat{v}}} Cov(u,v)$$

where $\hat{u}=\mathrm{E}(u)$, $\hat{v}=\mathrm{E}(v)$ and the partial derivatives of $f(u,v)$ are evaluated at $u=\hat{u}$ and $v=\hat{v}$.

So we need to compute the second-order derivatives of $f$, and also the moments $\mathrm{E}(u)$, $\mathrm{E}(v)$, $Var(u)$, $Var(v)$, $Cov(u,v)$.

The second-derivatives are as follows:

$$\frac{\partial^2 f}{\partial u^2} = \frac{-3uv}{(u^2+v)^{5/2}} \mathrm{;} \frac{\partial^2 f}{\partial v^2} = \frac{3u}{4(u^2+v)^{5/2}} \mathrm{;} \frac{\partial^2 f}{\partial u \partial v} = \frac{u^2-\frac{v}{2}}{(u^2+v)^{5/2}}$$

Then, the moments of $u$ are the moments of $X_i$, so $\hat{u}=\mu_i$ and $Var(u)=\Sigma_{i,i}$. The moments involving $v$ can be obtained using moments of quadratic forms. Because $v$ is just a sum of squares of $X$ removing $X_i$, we denote $\mu_v$ the vector $\mu$ with element $i$ removed, and $\Sigma_v$ the matrix $\Sigma$ with row and column $i$ removed, for readable formulas. Then the formulas for the moments of $v$ are:

$$\hat{v} = \mathrm{E}(v) = tr(\Sigma_v) + \mu_v' \mu_v = \sum_{j\neq i} \left( \mu_j^2 + \Sigma_{j,j} \right)$$

$$Var(v) = 2 tr(\Sigma_v \Sigma_v) + 4\mu_v \Sigma_v \mu_v$$

For $Cov(u,v)$, we can use the formula for the covariance between a quadratic form $X' A X$ with $A\in \mathbb{R}^{n \times n}$ and a linear form $a'X$ with $a \in \mathbb{R}^{n}$. We set $A$ to be $1$ on the diagonal entries other than $i,i$, and 0 elsewhere (i.e. the identity matrix with a 0 in the $i$th diagonal element), and we set $a$ to be $1$ in entry $i$ and $0$ elsewhere. Then we have that:

$$Cov(u,v) = \sum_{j \neq i} \mu_j \Sigma_{j,i}$$

Thus, to find $\mathrm{E}\left( \frac{X_i}{||X||} \right)$ we compute the moments above, evaluate $f$ and its second derivatives at $(\hat{u},\hat{v})$, and just plug in the terms into the Taylor approximation formula.

For the case of diagonal $\Sigma$ (where $\Sigma_{j,j} = \sigma_j^2$) the expressions simplify:

$$Var(v) = \sum_{j=1}^{j=n} \left[ 2 \sigma_j^4 + 4\mu_j^2 \sigma_j^2 \right] - 2\sigma_i^4 - 4\mu_i^2\sigma_i^2 $$ $$Cov(u,v)=0$$

then, nice, efficient vectorized formulas can be used to compute $\mathrm{E}\left( \frac{X}{||X||} \right)$. Maybe there's also nice vectorized formulas for the non-diagonal $\Sigma$ case, I haven't tried to solve through that yet.

The method works remarkably well in the cases I've tried so far (with diagonal $\Sigma$).

Answer 2

Here are two special cases that might be used to check on the Taylor series approximations a bit faster and more accurate than using simulations (using Mathematica).

Special case: $n=2$.

Suppose $X_i\sim N(\mu_i,\sigma_i^2)$ for $i=1,2$. We find the joint density for $Z_1=X_1/\sqrt{X_1^2+X_2^2}$ and $Z_2=\sqrt{X_1^2+X_2^2}$ from which we find the marginal density for $Z_1$ and then use numerical integration to find the mean of $Z_1$.

(* Format indexed variables for output to be more readable *)
Format[x[n_]] := Subscript[x, n]
Format[z[n_]] := Subscript[z, n]
Format[μ[n_]] := Subscript[μ, n]
Format[σ[n_]] := Subscript[σ, n]
(* Define joint distribution *)
dist = TransformedDistribution[{x[1]/Sqrt[x[1]^2 + x[2]^2], 
    Sqrt[x[1]^2 + x[2]^2]},
   {x[1] [Distributed] NormalDistribution[μ[1], σ[1]], 
    x[2] [Distributed] NormalDistribution[μ[2], σ[2]]}];
(* Joint pdf of z[1]=x[1]/Sqrt[x[1]^2+x[2]^2] and z[2]=Sqrt[x[1]^2+x[2]^2] *)
jointPDF = PDF[dist, {z[1], z[2]}][[1, 1, 1]]

(* Marginal pdf of z[1] by integrating out z[2] *)
a = {μ[1] ∈ Reals, μ[2] ∈ Reals, σ[1] > 0, σ[2] > 0, -1 < z[1] < 1};
pdfz1 = FullSimplify[Integrate[jointPDF, {z[2], 0, ∞}, Assumptions -> a],  Assumptions -> a]

(* For any specific values of the parameters one can use numerical integration to find the mean *)
parms = {μ[1] -> 4, μ[2] -> 3, σ[1] -> 2, σ[2] ->  1/2};
mean = NIntegrate[z[1] pdfz1 /. parms, {z[1], -1, 1}]
(* 0.7233206280335711 *)

Special case: $n>1$ and $\sigma_i^2=\sigma_2^2$ for $i=2,\ldots,n$

Here we have $X_1\sim N(\mu_1,\sigma^2_1)$ and $X_i\sim N(\mu_i,\sigma^2_2)$ for $i=2,\ldots,n$. We define $V=\sum_{i=2}^n X_i^2$ where $V$ has a noncentral $\chi^2$ distribution with parameters $n-1$ and $\lambda=\sum_{i=2}^n \mu_i^2$. So $Z_1=X_1/\sqrt{X_1^2+V}$ and $Z_2=\sqrt{X_1^2+\sigma_2^2 V}$. We find the joint density of $Z_1$ and $Z_2$. With specific parameters there is a closed-form for the marginal density of $Z_1$ but it's messy and numerical integration is still necessary to find the mean of $Z_1$. So we set parameters and numerically integrate the joint distribution of $Z_1$ and $Z_2$.

dist1 = TransformedDistribution[{x[1]/Sqrt[x[1]^2 + σ[2]^2 v], 
    Sqrt[x[1]^2 + σ[2]^2 v]},
   {x[1] \[Distributed] NormalDistribution[μ[1], σ[1]],
    v \[Distributed] NoncentralChiSquareDistribution[n - 1, Sum[μ[i]^2/σ[2]^2, {i, 2, n}]]}];
jointPDF = FullSimplify[PDF[dist1, {z1, z2}][[1, 1, 1]],
  Assumptions -> {z2 > 0, -1 < z1 < 1, σ[1] > 0, σ[2] > 0}]

(* Set parameters *)
parms = {n -> 4, μ[1] -> 2, μ[2] -> 3, μ[3] -> 1/2, μ[4] -> 5, σ[1] -> 3, σ[2] -> 4};
(* Perform numerical integration *)
integrand = z1 jointPDF //. parms

mean = NIntegrate[integrand, {z1, -1, 1}, {z2, 0, ∞}]
(* 0.216965 *)
(* Check with simulations )
SeedRandom[12345];
nsim = 1000000;
x1 = RandomVariate[NormalDistribution[μ[1], σ[1]] /. parms, nsim];
x2 = RandomVariate[NormalDistribution[μ[2], σ[2]] /. parms, nsim];
x3 = RandomVariate[NormalDistribution[μ[3], σ[2]] /. parms, nsim];
x4 = RandomVariate[NormalDistribution[μ[4], σ[2]] /. parms, nsim];
Mean[x1/Sqrt[x1^2 + x2^2 + x3^2 + x4^2]]
( 0.216869 *)