Model predictions are under-predicting on the high end of the distribution

Question

I am trying to create a linear model where the dependent variable has the following summary features:

Min	1st Qu.	Median	Mean	3rd Qu.	Max
0.1579	0.3155	0.3547	0.3459	0.3827	0.4583

There were some notable outliers on both ends, so I used a robust linear regression. In training the model, I logged both the dependent variable and the two main features feeding into the model, and the resulting predictions had the following skew:

After experimenting with a beta regression using the betareg package, the results look much better on the low end of the predictions, but the model still systematically under-predicts on the high end. Any suggestions?

As Dave noted below, here is a better representation of the problem I laid out - the model is systematically under-predicting on the high end.

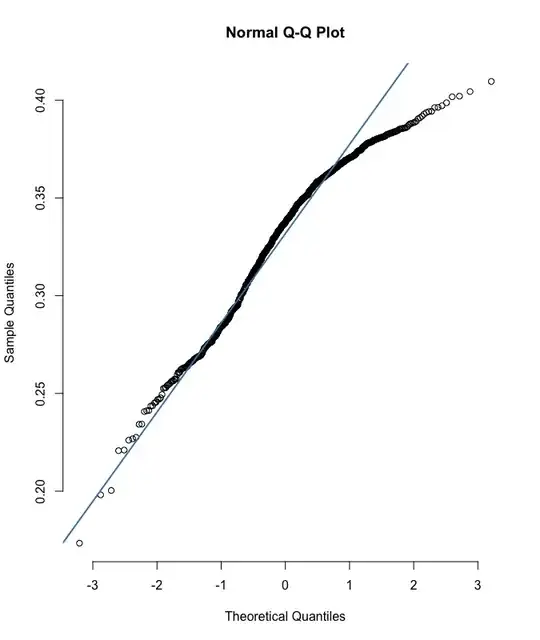
Welcome to Cross Validated! What's wrong with having skewed predictions? There is no reason to expect the predictions to be normal. Some R code demonstrates that. set.seed(2023); N <- 1000; x <- rbeta(N, 5, 1); e <- rnorm(N, 0, 1); y <- 14*x + e; L <- lm(y ~ x); yhat <- predict(L); qqnorm(yhat); qqline(yhat) The y here seems to have the same kind of skew as yours has. — Dave, Nov 01 '23 at 16:53
In this case, it's more important to have accurate predictions in the 0.38 - 0.45 range than it is for there to be precision in the 0.25 - 0.35 range. Do you have any suggestions for how to amend my modeling process or make a change in post-processing that achieves that? — BSHuniversity, Nov 01 '23 at 16:55
What do you mean when you say you 'logged' the variables. Did you apply the logarithm? If yes, why? — ChrisL, Nov 01 '23 at 16:57
I struggle to understand what your theoretical quantiles are. Are you simulating from a predictive density? Or are you taking quantiles from conditional expectation predictions? If the latter, you may be running afoul of the fact that predictions will almost always vary less than observations. — Stephan Kolassa, Nov 01 '23 at 17:00
I believe the duplicate addresses this. Please feel free to disagree (with justification). I'll gladly reopen if this question really does differ from that one. — Dave, Nov 01 '23 at 17:14

score 3 · Answer 1 · answered Nov 01 '23 at 17:04

The QQ plot says nothing about how well the predicted values align with the observed values. Therefore, you are using the wrong tool to assess the fit of your regression model.

What the QQ plot says is how well the values align with a normal distribution that has the empirical mean and variance. In this case, the answer is that your predicted values align rather poorly with such a distribution, but there is no reason to hope they do.

If you want a plot to check how well your observed and predicted values align with each other, plot those, such as I do below.

set.seed(2023)
N <- 1000
x <- rbeta(N, 5, 1)
e <- rnorm(N, 0, 1)
y <- 14*x + e
L <- lm(y ~ x)
yhat <- predict(L)
plot(
  yhat, y,
  xlab = "Predicted Values",
  ylab = "Observed Values"
)
abline(0, 1)

In this example, the predicted and observed values are quite close to each other.

I suggest doing this kind of plot in your work. The QQ plot answers a totally different question, one that does not seem important to your work.

Thanks for this info Dave. I updated the question with this info as I believe it is showing the same problem that I thought it might - on the high end of the model predictions, we are systematically under-predicting and on the low end (unimportant for us), we are over-predicting. — BSHuniversity, Nov 01 '23 at 17:08
Sometimes the distribution of the residual can inform improvements in the learner. I have found cases where Gaussian Mixture models fit it well, and I can chase those upstream to independent components of the system creating noise, and I can adjust them so that the overall variation is reduced. — EngrStudent, Nov 01 '23 at 18:05

Model predictions are under-predicting on the high end of the distribution

1 Answers1