Are there any stat libraries that show normal distributions across values of the theta

Question

I'm looking at the sensitivity of a hall-effect sensor and trying to characterize its abilities visually. Most sensor ranges or power ratios are dependent on the direction of the sensor and also a degree θ so you get lobes of various power settings or sensetivity depending on the broadcast/reception nature of the equipment.

I would like to look at detection power as a sort of torus. If you were to slice through a torus you would see a 2-D plot which could be interpreted as a probability density function for detection at distance (0.1 to 1.0 meters) from the sensor. My idea is to make my measurements and then show the sensitivity for every 2° around the sensor as a p.d.f. Then I tie them together as a surface to show where the majority of the detection is. It might look something like this.

My question is simply, has anyone ever seen a numpy or R library (really any library) that can do this kind of work BEFORE I have to go generate it myself? Otherwise I'm going to be building OpenGL surfaces with interesting vertex descriptions.

Maybe less important, but does anyone think this is a bad idea for statistical representation?

Added for clarity. I don't have a good example of what I want, but consider this image. If this were my plot (and it could be), then a p.d.f. along one of the radii might look like the plot on the right.

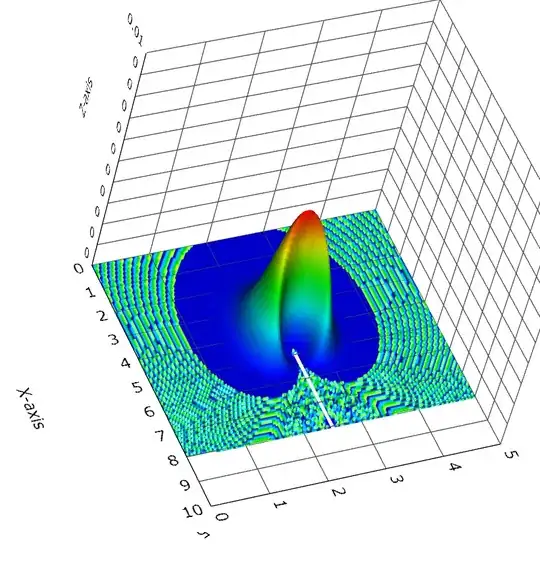
Final edit Partly this may just be a visualization thing and what I'm trying to do is novel enough that no one has an opinion on it. Let me try one more example as I have been trying to prototype the output I want.

Here i rapidly adopted a javascript surcase solution using webgl. I added a gamma distribution where the angle from my origin was β and the k=4. I got a swirl around the center. The 3-D plot shows a surface which is visually accessible. On the other hand if I were to slice from the center down any radius I would get a gamma distribution function.

I'm already halfway to a decent prototype, but my question still remains. Has anyone else done something like this and are there any drawbacks to this visualization of the data?

"I would like to look at detection power as a sort of torus" Could you explain why and what it is supposed to show. — Sextus Empiricus, Sep 12 '23 at 17:27
"If you were to slice through a torus you would see a 2-D plot which could be interpreted as a probability density function" If I slice a torus then I get some weird shape which can be all sorts, like circle, ellipse, banana or ring. What do you mean by 2d plot and by probability density function? — Sextus Empiricus, Sep 12 '23 at 17:30
@SextusEmpiricus if you would, prefer think of this as a surface rather than a torus. I'm thinking about something I can't depict well and I may be failing in describing it adequately. If you slice through a surface from the origin along some angle θ you would have some 2-d plot and it is my intention to use p.d.f.s in that capacity. So, the final product would be a 3-D plot manufactured by first inserting 360 degrees of p.d.f.s I'm not sure that clarifies. — BSD, Sep 12 '23 at 17:57
Is your torus something like this 3d pattern displayed on Wikipedia? https://commons.m.wikimedia.org/wiki/File:Radiation-patterns-v.png — Sextus Empiricus, Sep 12 '23 at 18:34
Is your question effectively "how to plot a surface based on radial coordinates?". Or in different words, how to produce the left image at the end of your post based on the slices in the right image at the end of your post. — Sextus Empiricus, Sep 12 '23 at 18:50
@SextusEmpiricus thanks, but no. I'm a programmer and I can build surfaces with several tools. My question related to the statistic visualization problem and I was hoping that someone had already done something like this. — BSD, Sep 12 '23 at 19:10
So you your question is not how to perform a specific visualisation, but instead what the visualisation could be? — Sextus Empiricus, Sep 12 '23 at 19:17
I am confused now. In your question you speak about "Then I tie them together as a surface" but in you last comment you state that the question is not about building a surface. What is it instead about in that case? — Sextus Empiricus, Sep 12 '23 at 19:20
Although I cannot make any sense of this, it seems you are seeking how to describe and visualize a probability distribution in the plane using polar coordinates. But I find it impossible to determine what this post is about: data, densities, polar coordinates, 2D distributions, visualization, circular distributions, maybe something else?? — whuber, Sep 12 '23 at 20:13

Sextus Empiricus · Accepted Answer · 2023-09-13T11:37:01.650

Is this a sort of visualisation that you are looking for? Based on the value of a function observed at points on a grid of radial coordinates, we plot the 'density'/value of that function

library(akima)
range of polar coordinates
theta = seq(1,360,2)/3602pi
r = seq(0,10,0.1)
matrix of cartesian coordinates
and some value of the surface height
z = outer(theta,r,FUN = function(theta,r) {cos(3theta)^2(1+cos(theta))dgamma(r,2,0.2)})10
x = outer(theta,r,FUN = function(theta,r) {cos(theta)r})
y = outer(theta,r, FUN = function(theta,r) {sin(theta)r})
interpolate to rectangular grid
data <- interp(x = x, y = y, z = z, duplicate = "mean")
contour plot
filled.contour(x = data$x,
               y = data$y,
               z = data$z,
               xlab = "x",
               ylab = "y",
               main = "example of contour plot \n based on originally radial data", cex.main = 1)

Direct plotting

My answer was not to suggest the use of interpolation, but more to inquire about the visualisation which was not so clear in the question. An alternative way of plotting would be to use the data directly on the circular grid

library(akima)
range of polar coordinates
theta = seq(2,360,2)/3602pi
deltar = 0.1
r = seq(0,10,deltar)
matrix of cartesian coordinates
and some value of the surface height
z = outer(theta,r,FUN = function(theta,r) {cos(3theta)^2(1+cos(theta))dgamma(r,2,0.2)})10
ctheta = outer(theta,r,FUN = function(theta,r) {theta})
cr = outer(theta,r, FUN = function(theta,r) {r})
empty plot
plot(-100,-100, xlim = c(-10,10), ylim = c(-10,10), xlab = "x", ylab = "y")
some color palette
zr = 1-z/max(z)
col = hsv(0.15+0.55zr,0.7-0.5zr,1-0.3*zr)
a for loop to plot all the individual facets
the question could be whether there's a library that can do this more efficiently
for (i in 1:length(z)) {
   dtheta = ctheta[i]+c(-1,1,1,-1,-1)/3602pi
   dr = cr[i]+c(-1,-1,1,1,-1)deltar/2
   dx = cos(dtheta)dr
   dy = sin(dtheta)*dr
   polygon(dx,dy,col=col[i], border = col[i])
}

A lower resolution with the grid lines plotted as well:

Maybe less important, but does anyone think this is a bad idea for statistical representation?

I have several concerns about the presented question.

I wonder whether plotting 3d surfaces is the best choice.

A 3d surface can give in some cases a clear idea, for example regarding the Bayes factor

example: https://stats.stackexchange.com/a/5858/

But it is also a visual representation that can obscure the view and interpretation. The information is not directly visible and it requires the viewer to interpret the 2D visualisation of the 3D plot. This is especially difficult for complex surfaces.
I also wonder about your use of the term PDF. That acronym translates as 'Probability Density Function', but it is not clear what sort of probability your are relating to.
Finally, what is the message that needs to be conveyed? Possibly a simpele 2d plot with a few lines can do this already?

Yes, this is very close to what I was looking for. What language is this? R? — BSD, Sep 12 '23 at 20:45
@BSD the language is in R. The trick is to use interpolation to get values on a rectangular grid. That may exist in other languages as well. The method may not work as nice when your data is noisy. --- Also, you could of course still create a function that plots the polar facets that you have (I am thinking about a graphic that I once made here https://stats.stackexchange.com/a/597617/ using TikZ, I don't remember the library, which I believe doesn't require the data points on a rectangular grid but instead the coordinates of all the facets individually. The difficult center could be left out. — Sextus Empiricus, Sep 13 '23 at 05:17

score 2 · Answer 2 · answered Sep 12 '23 at 21:01

2

Very similar to @Sextus Empiricus

Instead of contour, use persp(x = data$x, y = data$y, z = data$z)

answered Sep 12 '23 at 21:01

BSD

235

3d plots can be difficult to read. You might want to add the contours as well like here: https://stats.stackexchange.com/a/369909 – Sextus Empiricus Sep 13 '23 at 06:14

Are there any stat libraries that show normal distributions across values of the theta

Maybe less important, but does anyone think this is a bad idea for statistical representation?

2 Answers2

range of polar coordinates

matrix of cartesian coordinates

and some value of the surface height

interpolate to rectangular grid

contour plot

Direct plotting

range of polar coordinates

matrix of cartesian coordinates

and some value of the surface height

empty plot

some color palette

a for loop to plot all the individual facets

the question could be whether there's a library that can do this more efficiently