I'm trying to work out a linear regression model where both inputs and outputs are multidimensional.
Suppose we have $n$ input variables, $m$ output variables and $k$ observations. Each observation can be represented as an $n+m$-vector: $(x_1,...,x_n,y_1,...,y_m)$. The full set of observations can be represented with two matrices:
$X$ an $n\times k$ matrix of inputs. Each row is one input variable. Each column is one datapoint.
$Y$ an $m\times k$ matrix of outputs. Each row is one output variable. Each column is one datapoint.
The model can be summarized as $Y\approx AX+B$, where $A$ is an $m\times n$ matrix and $B$ is an $m$-vector (well technically, an $m$-vector copied $k$ times to form an $m\times k$ matrix). The goal is to find optimal values for $A$ and $B$.
I think the natural choice is to minimize $\sum_i \sum_j (y_{ij} - predicted(y_{ij}))^2$, i.e. the sum of squares with all output variables and all observations weighted equally. That is, $\sum_i \sum_j ((y_i-\sum_l a_{il}x_{lj})-b_i)^2$.
I worked it out and found that for any fixed $A$, the minimum occurs when $b_i=mean_j (y_{ij}) – \sum_l a_{il} mean_j (x_{lj})$.
The hard part is finding $A$. After plugging in the minimizing value of $B$, the function to be minimized is:  , where
, where
where $dx_{ij} = x_{ij} – mean_j(x_{ij}), dy_{ij}=y_{ij} – mean_j(y_{ij})$
This is a quadratic function in the entries of $A$. It attains its minimum precisely at its critical point(s). To find those, condense the $S^2_{ij}$ and $S^2_{ijj'}$ into a single $nm\times nm$ matrix:
Here we think of the pair of indices $ij$ as if it were a single index via a bijection between pairs of integers in $[1,n]\times [1,m]$ and integers in $[1,nm]$. Then minimizing values of $A$ are exactly given by solutions to the equation $S^2\vec{A}=-\frac{1}{2}S^1$, where $S^1$ is a column vector storing the $S^1_{ij}$ in the order given by that bijection and $\vec{A}$ is $A$ collapsed down to a single $nm$-length column vector via that same bijection.
$S^2$ is always positive semidefinite. If it is positive definite, then we're in the nice case of a single optimal solution $\vec{A}=(S^2)^{-1}(-\frac{1}{2}S^1)$. But if not, then I suppose we might get a positive-dimensional set of optimal solutions.
So my question is: Is there a nice theorem, preferably with a clear statistical interpretation, to tell when that matrix is not invertible? And can it be derived from the formulas above? Something analogous to the one-variable case, where the least-squares line breaks down iff var(X)=0, i.e. all the datapoints have the same input value.
Note: I found many results when searching for multivariable linear regression, but the ones I found all assumed only 1 output variable; so I had to derive this more general case myself. I did find one helpful reference on multivariable quadratic functions here
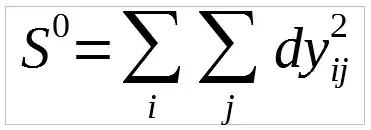


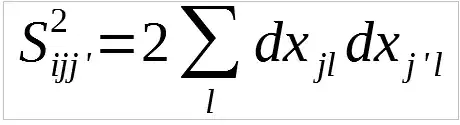

multivariaterefers to >1 outputs.multipleandmultivariable(I prefermultiple) refer to >1 inputs. Unfortunately, this terminology is just poor and there is lots of confusion around the terms. – mkt Aug 18 '23 at 06:43