I'm trying to model the relationship between two variables. Without going into details on how I get this expectation, my belief on the relationship between the variables looks like this:
However, as time advances I start to see instances of the true relationship. Early on, I might see something like this, where the orange points are observed.
You can see that the orange line is coming in a little lower than the blue. I'd like my predictions to account for this, and largely fit lower for small values of x but then continue on that upward trend for higher values of x that haven't been observed.
Later on in time, I might see additional points, like this:
At this point you can see that the y-values for even high values of x are clearly suppressed relative to my blue expectations. Again, I'd like the fit to go through those, while still turning upwards for the blue values at higher x.
What would be the best way to do this? I've thought of a number of approaches:
(1) I could just do a normal (non-Bayesian) regression fit where I weigh the prior points with lower weight, and then just do a new fit where my new points come in at higher weight.
(2) Some sort of Bayesian polynomial fit, where my prior curve truly is a prior and I'm doing Bayesian updates. I've never done this before, but there are examples online (bayesian_regression). However, I'm not familiar with the various noise-related parameters of the Bayesian fit to know clearly how I should approach this.
Suggestions on how I might proceed? For the record, the relationship between x and y for the blue points is not a clean polynomial (I can get a decent approximation of the line with a high order polynomial, but it's far more wiggly than I'd like). A tree-based method could fit those points better, which means I could opt for a weight-based solution like (1) but with trees with weights (since I definitely don't know how to build a tree-based solution with a Bayesian approach). I'd love to receive advice either with this fact included or would also be very interested in answers where one assumed that the blue points were represented well by some simple lower-order polynomial.
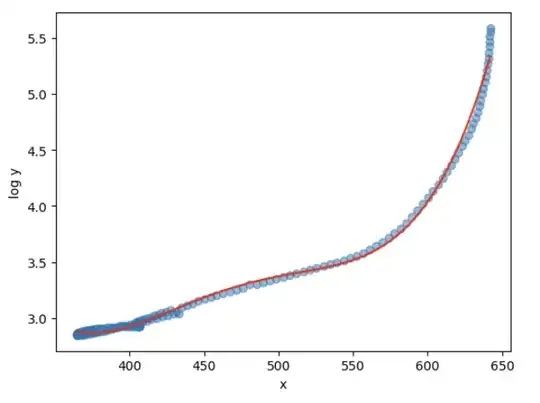
Edit: @Durden suggested that I consider modeling the relationship as a log-linear model. That looks like that is indeed helpful, as you can see the fit on a 4th order polynomial between x and log y is very good.