I want to fit a beta regression with an scaled continuous predictor, and express the slope in terms of proportion (not at the transformed, log-odds scale). In other words, I would like to express the change in the response variable (a proportion), when the predictor increases 1 standard deviation from the mean.
I can get the slope at the probability scale with the emmeans::emtrends() function, but I don't know how to do it manually from the model output. In contrast, I can back-transform and interpret intercepts and factor coefficients manually, or so I think. The fact that I cannot do the same for an scaled continuous predictor suggests I don't understand my model very well. Can anyone shed light on this?
I have found some inspiration in previous questions here, here and here.
See below a reproducible example, showing manual calculation of intercepts, factor coefficients, and slopes.
Note that emmeans::emtrends() appears to take the scaling into account only when it is done in the input data, not on the model formula.
library(betareg)
library(effects)
#> Loading required package: carData
#> lattice theme set by effectsTheme()
#> See ?effectsTheme for details.
library(emmeans)
library(glmmTMB)
library(tidyverse)
#> Warning: package 'ggplot2' was built under R version 4.2.2
#> Warning: package 'tibble' was built under R version 4.2.3
#> Warning: package 'tidyr' was built under R version 4.2.3
#> Warning: package 'purrr' was built under R version 4.2.3
#> Warning: package 'dplyr' was built under R version 4.2.3
#> Warning: package 'stringr' was built under R version 4.2.3
library(visreg)
######### Dataset
data("FoodExpenditure", package = "betareg")
FoodExpenditure$resp <- FoodExpenditure$food / FoodExpenditure$income
FoodExpenditure$income.s <- as.numeric(scale(FoodExpenditure$income))
summary(FoodExpenditure)
#> food income persons resp
#> Min. : 7.431 Min. :25.91 Min. :1.000 Min. :0.1075
#> 1st Qu.:11.069 1st Qu.:42.12 1st Qu.:2.000 1st Qu.:0.2269
#> Median :14.831 Median :60.45 Median :3.000 Median :0.2611
#> Mean :15.953 Mean :58.44 Mean :3.579 Mean :0.2897
#> 3rd Qu.:19.102 3rd Qu.:76.79 3rd Qu.:5.000 3rd Qu.:0.3469
#> Max. :28.980 Max. :88.23 Max. :7.000 Max. :0.5612
#> income.s
#> Min. :-1.6326
#> 1st Qu.:-0.8192
#> Median : 0.1007
#> Mean : 0.0000
#> 3rd Qu.: 0.9206
#> Max. : 1.4945
######### The back-transformed intercept from a null model coincides with the sample mean
mean(FoodExpenditure$resp)
#> [1] 0.2896702
summary(glmmTMB(resp ~ 1, data = FoodExpenditure, family = beta_family(link = "logit"), dispformula = ~ 1))
#> Family: beta ( logit )
#> Formula: resp ~ 1
#> Data: FoodExpenditure
#>
#> AIC BIC logLik deviance df.resid
#> -66.7 -63.4 35.3 -70.7 36
#>
#>
#> Dispersion parameter for beta family (): 20.9
#>
#> Conditional model:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -0.8925 0.0763 -11.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
plogis(- 0.8925)
#> [1] 0.2905942
######### Factors: back-transformed coefficients coincide with raw probabilities calculated from the data
mod.factor <- glmmTMB(resp ~ factor(persons), data = FoodExpenditure, family = beta_family(link = "logit"), dispformula = ~ 1)
summary(mod.factor)
#> Family: beta ( logit )
#> Formula: resp ~ factor(persons)
#> Data: FoodExpenditure
#>
#> AIC BIC logLik deviance df.resid
#> -66.4 -53.3 41.2 -82.4 30
#>
#>
#> Dispersion parameter for beta family (): 28.5
#>
#> Conditional model:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -1.06718 0.20873 -5.113 3.17e-07 ***
#> factor(persons)2 -0.09564 0.25723 -0.372 0.71003
#> factor(persons)3 0.21242 0.25180 0.844 0.39889
#> factor(persons)4 -0.01733 0.28018 -0.062 0.95068
#> factor(persons)5 0.26137 0.25112 1.041 0.29796
#> factor(persons)6 0.77294 0.29930 2.582 0.00981 **
#> factor(persons)7 0.45845 0.34230 1.339 0.18046
#> ---
#> Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Raw probabilities from the data
FoodExpenditure %>% group_by(persons) %>% summarise(mean = mean(food/income)) %>% pull(mean)
#> [1] 0.2491281 0.2317299 0.2947887 0.2564000 0.3130861 0.4256767 0.3675447
Back-transformed probabilities from the model: manually or through estimated marginal means
plogis(c(coef(summary(mod.factor))$cond[1, 1], (coef(summary(mod.factor))$cond[1, 1] + coef(summary(mod.factor))$cond[-1, 1])))
#> factor(persons)2 factor(persons)3 factor(persons)4
#> 0.2559398 0.2381552 0.2984353 0.2526537
#> factor(persons)5 factor(persons)6 factor(persons)7
#> 0.3087838 0.4269665 0.3523495
summary(emmeans::emmeans(mod.factor, specs = ~ persons, regrid = "response"))$response
#> [1] 0.2559398 0.2381552 0.2984353 0.2526537 0.3087838 0.4269665 0.3523495
######### Continuous
mean(FoodExpenditure$income)
#> [1] 58.44434
sd(FoodExpenditure$income)
#> [1] 19.93156
Compare models with and without scaling, and with the scaling done in the model formula or in the data frame
list.model <-
list(
"not.scaled" = glmmTMB(resp ~ income, data = FoodExpenditure, family = beta_family(link = "logit"), dispformula = ~ 1),
"scaled" = glmmTMB(resp ~ scale(income), data = FoodExpenditure, family = beta_family(link = "logit"), dispformula = ~ 1),
"scaled.df" = glmmTMB(resp ~ income.s, data = FoodExpenditure, family = beta_family(link = "logit"), dispformula = ~ 1)
)
Model coefficients
lapply(list.model, function(x) coef(summary(x))$cond[, 1])
#> $not.scaled
#> (Intercept) income
#> -0.21032876 -0.01187883
#>
#> $scaled
#> (Intercept) scale(income)
#> -0.9045793 -0.2367637
#>
#> $scaled.df
#> (Intercept) income.s
#> -0.9045793 -0.2367637
Coefficients transformed to probabilities by undoing the logit link: scaling yields an intercept that coincides with the sample mean of the response variable (since scaled variables are also centered).
However, the scaled slope is less straightforward
lapply(list.model, function(x) plogis(coef(summary(x))$cond[, 1]))
#> $not.scaled
#> (Intercept) income
#> 0.4476108 0.4970303
#>
#> $scaled
#> (Intercept) scale(income)
#> 0.2881104 0.4410840
#>
#> $scaled.df
#> (Intercept) income.s
#> 0.2881104 0.4410840
Estimated trends at probability scale: scaling only taken into account if declared in the data frame and not in the model's formula
lapply(list.model[1:2], function(x) emmeans::emtrends(x, specs = ~ income, var = "income", regrid = "response"))
#> $not.scaled
#> income income.trend SE df lower.CL upper.CL
#> 58.4 -0.00244 0.000706 35 -0.00387 -0.001
#>
#> Confidence level used: 0.95
#>
#> $scaled
#> income income.trend SE df lower.CL upper.CL
#> 58.4 -0.00244 0.000706 35 -0.00387 -0.001
#>
#> Confidence level used: 0.95
emmeans::emtrends(list.model$scaled.df, specs = ~ income.s, var = "income.s", regrid = "response")
#> income.s income.s.trend SE df lower.CL upper.CL
#> -9.39e-17 -0.0486 0.0141 35 -0.0771 -0.02
#>
#> Confidence level used: 0.95
The slope could also be calculated manually at the probability scale from a visualization of the model. However, this is prone to error and hardly practical.
visreg(list.model$scaled, "income", scale = "response")
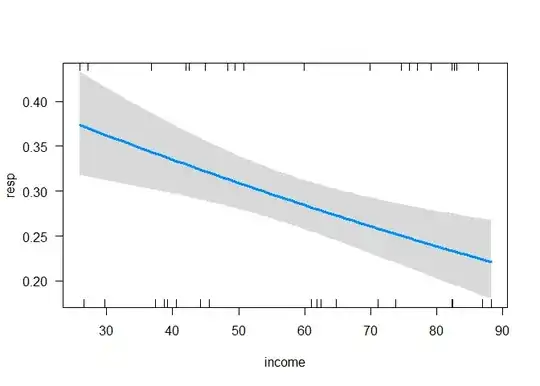
# Slope, not scaled
(0.375-0.225)/(max(FoodExpenditure$income) - min(FoodExpenditure$income))
#> [1] 0.002406623
# Slope, scaled
(0.375-0.225)/((max(FoodExpenditure$income) - min(FoodExpenditure$income))/sd(FoodExpenditure$income))
#> [1] 0.04796776
sessionInfo()
#> R version 4.2.0 (2022-04-22 ucrt)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 22000)
#>
#> Matrix products: default
#>
#> locale:
#> [1] LC_COLLATE=Spanish_Spain.utf8 LC_CTYPE=Spanish_Spain.utf8
#> [3] LC_MONETARY=Spanish_Spain.utf8 LC_NUMERIC=C
#> [5] LC_TIME=Spanish_Spain.utf8
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] visreg_2.7.0 forcats_0.5.1 stringr_1.5.0
#> [4] dplyr_1.1.2 purrr_1.0.1 readr_2.1.2
#> [7] tidyr_1.3.0 tibble_3.2.1 ggplot2_3.4.0
#> [10] tidyverse_1.3.1 glmmTMB_1.1.3 emmeans_1.8.5-9000004
#> [13] effects_4.2-1 carData_3.0-5 betareg_3.1-4
#>
#> loaded via a namespace (and not attached):
#> [1] nlme_3.1-157 fs_1.5.2 lubridate_1.8.0
#> [4] insight_0.19.1.3 httr_1.4.3 numDeriv_2016.8-1.1
#> [7] tools_4.2.0 TMB_1.8.1 backports_1.4.1
#> [10] utf8_1.2.2 R6_2.5.1 DBI_1.1.2
#> [13] colorspace_2.0-3 nnet_7.3-17 withr_2.5.0
#> [16] tidyselect_1.2.0 compiler_4.2.0 cli_3.6.1
#> [19] rvest_1.0.2 xml2_1.3.3 sandwich_3.0-1
#> [22] scales_1.2.0 lmtest_0.9-40 mvtnorm_1.1-3
#> [25] digest_0.6.29 minqa_1.2.4 rmarkdown_2.14
#> [28] pkgconfig_2.0.3 htmltools_0.5.2 lme4_1.1-29
#> [31] dbplyr_2.1.1 fastmap_1.1.0 highr_0.9
#> [34] rlang_1.1.1 readxl_1.4.0 rstudioapi_0.13
#> [37] generics_0.1.2 zoo_1.8-10 jsonlite_1.8.0
#> [40] magrittr_2.0.3 modeltools_0.2-23 Formula_1.2-4
#> [43] Matrix_1.4-1 Rcpp_1.0.10 munsell_0.5.0
#> [46] fansi_1.0.3 lifecycle_1.0.3 stringi_1.7.6
#> [49] multcomp_1.4-19 yaml_2.3.5 MASS_7.3-57
#> [52] flexmix_2.3-17 grid_4.2.0 crayon_1.5.1
#> [55] lattice_0.20-45 haven_2.5.0 splines_4.2.0
#> [58] hms_1.1.1 knitr_1.39 pillar_1.9.0
#> [61] boot_1.3-28 estimability_1.4.1 codetools_0.2-18
#> [64] stats4_4.2.0 reprex_2.0.2 glue_1.6.2
#> [67] evaluate_0.15 mitools_2.4 modelr_0.1.8
#> [70] vctrs_0.6.3 nloptr_2.0.1 tzdb_0.3.0
#> [73] cellranger_1.1.0 gtable_0.3.0 assertthat_0.2.1
#> [76] xfun_0.31 xtable_1.8-4 broom_0.8.0
#> [79] survey_4.1-1 coda_0.19-4 survival_3.3-1
#> [82] TH.data_1.1-1 ellipsis_0.3.2
Created on 2023-08-01 with reprex v2.0.2