Two dimensional random variable with uniform marginal probability density functions

Question

I have access to some data for two variables - let's call them x and y. In particular, I have the distribution of data separately per each variable, something that allows me to estimate the marginal distribution for each variable - let's call them $f_x(x)$ and $f_y(y)$. From those histograms I see that both variables have a marginal distribution which is uniform: $x \sim f_x(x)=\frac{1}{x_b-x_a}$ and $y \sim f_y(y)=\frac{1}{y_b-y_a}$, where of course $$f_x(x)=\int_{y_a}^{y_b}dy f(x,y)$$ $$f_y(y)=\int_{x_a}^{x_b}dx f(x,y) $$

Can we conclude that the full pdf $f(x,y)$ is the product of the two marginals or at least a pdf exists such that its marginals distributions are uniform?

Many thanks in advance and kind regards.

Answer 1

There is independence if and only if the product of the margins equals the joint density. You can find this shown in a classic book like Casella/Berger’s Statistical Inference.

Thus, you are asking if the two distributions are guaranteed to be independent. The answer is that they are not guaranteed to be independent. They might be, but they might not be.

For some additional reading, you might be interested in the concept of a copula.

EDIT

It is fairly easy to construct a joint distribution with uniform margins that has considerable dependence, meaning that the joint distribution is not just the product of the margins. I will give a suggestive simulation below. Fleshing out the theoretical mathematics would mean getting into copulas.

library(ggplot2)
library(MASS)
set.seed(2023)
N <- 100
Simulate some dependent data
Will form an X shape

d0 <- MASS::mvrnorm(
    N,
    c(0, 0),
    matrix(
        c(
            1, 0.99,
            0.99, 1
        ), 2, 2
    )
)
d1 <- MASS::mvrnorm(
    N,
    c(0, 0),
    matrix(
        c(
            1, -0.99,
            -0.99, 1
        ), 2, 2
    )
)
d <- rbind(d0, d1)
#Transform the margins to be U(0, 1)

x <- ecdf(d[, 1])(d[, 1])
y <- ecdf(d[, 2])(d[, 2])
Make data frames of the CDFs of the transformed x and y

df0 <- data.frame(
    Value = x,
    Quantile = ecdf(x)(x),
    Margin = "X"
)
df1 <- data.frame(
    Value = y,
    Quantile = ecdf(y)(y),
    Margin = "Y"
)
df_full <- rbind(df0, df1)
Plot the margins to show they are uniform

ggplot(df_full, aes(x = Value, y = Quantile)) +
    geom_point() +
    geom_line() +
    geom_abline(slope = 1, intercept = 0) +
    facet_grid(~ Margin)
Make a data frame for a scatter plot

df_scatter <- data.frame(
    X = x,
    Y = y
)
Plot the joint distribution as a scatter plot

ggplot(df_scatter, aes(x = X, y = Y)) +
    geom_point()

The margins are $U(0, 1)$.

The joint distribution shows dependence.

Independence would look more like this.

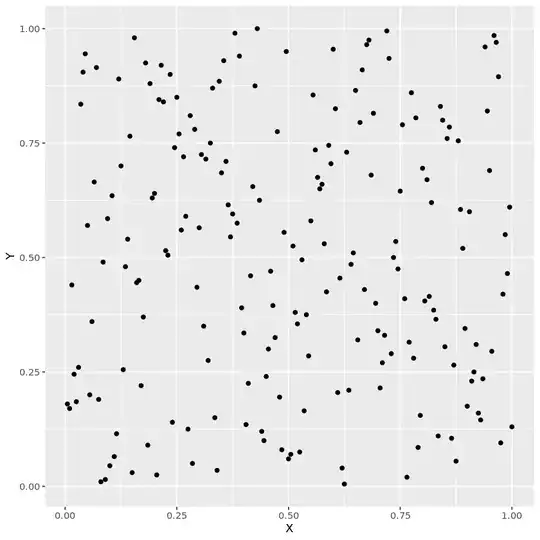
You can create this by using sample(y) in the df_scatter, which breaks the dependence structure by scrambling the y values.

(I’ve actually used a concept from copulas to create this example, and readers will be able to pick up on it if they know copulas and the ecdf function, though the key point is that, regardless of how I created the joint distribution, the margins are uniform yet dependent.)