Inference for high dimensional models based on running a (G)LM on the union of selected variables across best subset fits on bootstrapped datasets

Question

I am in the process of developing an R package for best subset selection, which approximates the best subset using an iterative adaptive ridge regression procedure (with the weighted least squares regression of the IRLS algorithm replaced by an adaptive ridge regression; I am also allowing for possible box constraints on my coefficients, in which case I use the osqp quadratic programming solver for this) (see Frommlet & Nuel 2016 & Li et al. 2021). This produces a stable approximation of the best subset, also for high dimensional cases (with many more variables than cases), but does not readily allow for inference, as there is no closed-form formula for the variance-covariance matrix of my iterated adaptive ridge coefficients (as far as I am aware). The optimal level of regularisation is chosen based on information criteria like mBIC, EBIC or cross validation. Now I was wondering - would it be OK to repeatedly bootstrap my dataset, do variable selection on each using my iterative adaptive ridge method & then identify the union of selected variables across these bootstrapped datasets, repeating this until the union of selected variables no longer grows, and then refitting a regular GLM on this union of selected variables using base R's function to provide inference (or https://rdrr.io/cran/zetadiv/man/glm.cons.html in case I have nonnegativity constraints)? Would anyone know if something like this has ever been suggested in the literature - I thought I had seen some suggestion along these lines in one of the Tibshirani articles on selective inference (in the context of LASSO), but I can't seem to find it now... Would anyone have any pointers? The suggestion almost seems too simple that it would surprise me if no one every tried it...

I've seen plenty of course that do least squares or a GLM on variables selected using LASSO, which is wrong as it doesn't take into account the uncertainty of the variable selection (ie it would be conditional on the set of selected variables being the correct ones - maybe bootstrapping could also help to identify whether that is a reasonable assumption - often not I would think). But by using the union of selected variables I thought I would not inflate the type I error rate & avoid this problem. I also had hoped that I would be able to determine a reliable union of selected variables based on a relatively limited number of bootstrap replicates (e.g. 100) and then subset my data to those variables to do a large number of bootstrap replicates (e.g. 10000) & fits to be able to do inference directly using the bootstrapped coefficients (which would then be much faster than using the full dataset). Any pointers perhaps to any work that did things this way?

EDIT: On my github I had a quick try to see if the method I propose would work, and it seems that I can do something similar to the bolasso, where variables are selected threshold% of the time to achieve asymptotic variable selection consistency, and where in the case of my L0 iterative adaptive ridge GLM algorithm a threshold of 30% works well, while for the group LASSO variables selected 70% of the time worked best (otherwise the selected set grows too large - for lasso 90% was the suggested threshold, but for best subset the threshold could be taken much lower as we expected false positives to enter the model only 5% of the time).

Here an example: if I regress a blurred multichannel spike train against a banded covariate matrix with time shifted copies of the known point spread function / blur kernel, with true coefficients I can recover the true support near-perfectly (which is not so obvious that that should be the case if you look at the raw data) Using a lambda chosen a priori that would maximise the GIC it can be seen that the correct support size is identified whilst also producing unbiased coefficients 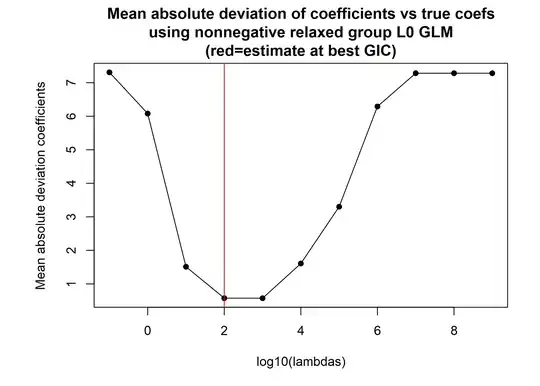and recovering the true support perfectly accurately (I was always told there should be a bias-variance tradeoff, but seems I can avoid it here - kind of magic)

If I do repeated fits on bootstrapped datasets & look at how the union of selected variables changes you can see that there is two plateaus, the first corresponding to the approximation of the true support (plus 3 or 4 nearly collinear variables) and a second one where false positives also start to level off (fairly quickly by the looks of it, reaching 35 out of 200 variables after 100 bootstrap replicates for a true support size of 20).

We do not get consistent variable selection in this way though - the set obviously grows slightly too big. But if it's OK to include some false positives then we could use a time-to-event analysis, e.g. using a survival analysis like flexsurvreg (allowing for 2 sets, true positives & false positives both selected relatively quickly and true negatives and some false negatives that are never selected) or flexmix (allowing for 3 sets, true positives selected quickly, false positives selected more slowly & true negatives plus some false negatives that are never selected), to calculate how many bootstrap replicates we would need to do to achieve a given coverage of the full asymptotic set that could ever be selected. The set could then be used to subset to when doing further fits on bootstrapped data, which would be fast given that fits using 35 variables would be way faster than fitting on the full dataset with 200 variables & then using the obtained coefficients directly to do inference. If the aim is just to get the best possible estimate of the true support or have a model with optimal prediction performance or optimal support then we can select variables that are selected at least x% of the time. In this case, 30% of the time works well, and with that threshold we get a near-perfect set of variables, with 20 selected variables, 19 of which are in the true set, and the 20th is still highly collinear with the true one (the best threshold to use could be optimised via cross validation or based on optimising an information criterion like AIC for optimal prediction performance or BIC for optimal variable selection consistency).

This set of selected variables that closely approximates the true set could then be put in the glm.cons function of the zetadiv package (fitting a GLM subject to nonnegativity constraints) or the regular R lm or glm function to provide inference. Or could be used as a subset to do nonparametric inference using bootstrapping.

Doing the same with a nonnegative group LASSO shows that there the union of the variables selected over different bootstrapped datasets would keep on growing much faster (which is not so surprising given that as such it does not enjoy selection consistency):

However, as suggested in the bolasso, we can select variables that appear at least threshold% of the time, with 70% here giving good results, resulting in the selection of 17 variables, all of which appear in the true set of 20 variables with nonnegative coefficients (so just 3 false negatives - worse than with the group L0 GLM method above).

But the set of variables selected by L0 glm on bootstrapped datasets converges faster to the true set, and gets you closer to the ground truth with far fewer bootstrap replicates. The plain nonnegative group LASSO estimates returned by glmnet are also pretty bad :

Just sticking in all variables to be able to do inference as suggested below is not possible in my example, as n=p, certainly not without explicitly taking into account nonnegativity constraints :

Answer 1

Whenever you do feature selection and then proceed with downstream inferences as if you had not, you have made at least a little bit of a mistake. The downstream inferences through the standard techniques assume that your variables had been pre-specified instead of selected by a data-driven procedure that is subject to change based on fluctuations in the data. This is related to Harrell’s criticism $\#7$ here (this is based on statistical theory and has nothing specific to Stata) and leads to criticisms $1$ through $4$.

Whether or not your approach is robust to this is not clear but could be studied with simulations to at least give a feel for how well it works (even if such evidence is just suggestive instead of a mathematical proof). My suspicion is that the robustness will be lackluster, but I am open to being wrong about that. (Such a result might even warrant dissemination in a more formal venue than Cross Validated, such as a publication, especially if it can be accompanied with some theoretical arguments.)

I have a few concerns about this procedure.

1. If you union over the selected features in your selection steps, you will wind up selecting features that only occasionally get selected. This procedure might not provide the level of selection that you desire, and you might wind up with just about all of the variables in the final model.
2. If you do get sparse models with few false positives (as your comment suggests you expect), there could be a large amount of false negatives: features that do matter but are excluded from the selection. This could result in underpowered testing, where your variable of interest might not even make it to the final model for formal inference steps, even if it does influence the outcome.
3. Omitting variables can lead to omitted-variable bias in your estimates.
4. I am skeptical of there being a benefit to such a procedure over sticking all of the variables in the model and doing the testing. If you want this to be “Wenseleers’s procedure” that others use, I think you need to make a more compelling argument about why there is a benefit to doing this, since there are a number of possible (perhaps even likely) drawbacks.