2

Let $\mathcal{L}(\theta\mid x_1,\ldots,x_n)$ be the likelihood function of parameters $\theta$ given i.i.d. samples $x_i$ with $i=1,\ldots,n$.

I know that under some regularity conditions the $\theta$ that maximizes $\mathcal{L}$ converges in probability to the true value $\theta_0$ as the sample size becomes infinite (i.e., the MLE is consistent). However, this does not mean that the likelihood for other values of $\theta$ is $0$: it just means that all those other values will be less than the one attained at $\theta=\theta_0$.

My question is whether the likelihood actually becomes $0$ in the limit when $n \to \infty$ for all values $\theta \neq \theta_0$.

I suppose that in order for this to hold (if it does), some regularity conditions would be required (possibly the same ones required to claim that the MLE is consistent and asymptotically efficient). Feel free to consider just the cases in which such conditions are met.

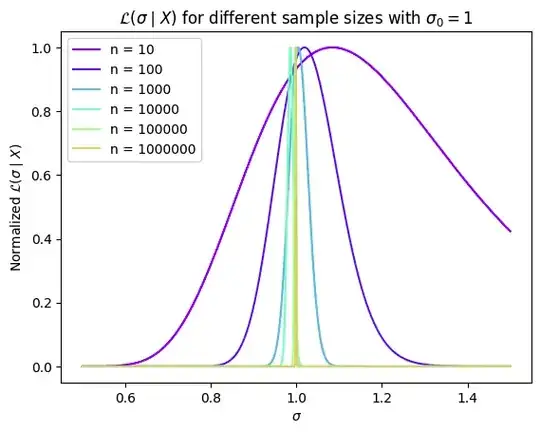
EDIT: Maybe the question is too general to be answered, so I want to specify that I am working with the covariance matrix of a multivariate Gaussian, nothing too fancy. In particular, for a one-dimensional random variable, I see that the behavior I described above is apparently true:

enter image description here

The problem is that I do not know how to describe this behavior mathematically. I mean, considering distributions like the Gaussian that meet the necessary regularity conditions, what does the likelihood function converge to when $n \to \infty$?

Tendero
  • 956
  • 8
  • 22
  • 3
    Interesting question, but without renormalization, I suspect that there will be many situations where the likelihood function diverges to infinity in certain regions (just slower than the divergence at $\theta$). Note that we need the density there to be $<1$ on average to get convergence to zero. Likewise, there are situations where the likelihood function $<1$ everywhere, and hence it will converge to zero even at $\theta$ (just slower than anywhere else). My guess. – John Madden May 19 '23 at 14:21
  • 1
    The definition of $\delta$ is in terms of its integral. Thus, for such convergence to hold, you must contemplate integrating $\mathcal L$ with respect to $\theta.$ This points the way towards minimal regularity conditions, because it must make sense to integrate the parameters and those values must be well defined and (generally) finite in the first place. – whuber May 19 '23 at 14:34
  • 1
    Check this answer at to why the likelihood function is not a probability density. – Xi'an May 19 '23 at 14:43
  • @JohnMadden I see your point, it makes complete sense. I have edited the question, hopefully now it is more accurate. – Tendero May 19 '23 at 15:04
  • @whuber Thanks to your comment I realized the likelihood function did not have a reason to integrate any specific value, so I edited the question to avoid the use of $\delta$. I think now it makes more sense. – Tendero May 19 '23 at 15:06
  • 1
    Perhaps another way of asking this question is whether the likelihood ratio $\frac{\mathcal{L}(\theta)}{\mathcal{L}(\theta')}$ diverges to infinity, which we can answer in the affirmative by appeal to hypothesis testing theory. – John Madden May 19 '23 at 15:08

2 Answers2

7

The Bernstein–von Mises theorem provides the asymptotic form (under regularity conditions) of the likelihood function. The likelihood itself does not become zero for $\theta \ne \theta_0$, but the posterior probability does. Notice that the posterior probability is essentially the same as as the normalized likelihood in the limit $n \to \infty$, given a prior that is "regular enough" in the neighborhood of $\theta_0$.

In other words, the likelihood becomes a Gaussian function centered at the true parameter $\theta_0$ with covariance matrix given by $n^{-1}I(\theta_0)^{-1}$, where $I(\theta_0)$ is the Fisher information matrix. The width of the Gaussian consequentially tends towards zero when $n \to \infty$.

J. Delaney
  • 5,380
  • Would it be correct to say that if we take a flat improper prior for $\theta$, then the theorem claims that $\frac{\mathcal{L}(\theta \mid x_1,\cdots,x_n)}{p(x_1,\cdots,x_n)} \to 0 \quad \forall \theta \neq \theta_0$ as $n\to \infty$? – Tendero May 19 '23 at 15:49
  • Yes, with the caveat that the denominator might not be a actual probability if the prior is improper – J. Delaney May 19 '23 at 16:17
  • That's a pretty good description of the $\delta$ (generalized) function! – whuber May 19 '23 at 16:29
  • Note that this tells us nothing about the values of the likelihood function, only the relative values. The likelihood of values of $\theta$ not equal to $\theta_0$ can still go to both 0 and $\infty$. – Cliff AB May 20 '23 at 01:26
2

Without further restrictions, you can't say much about the likelihood function as $n \rightarrow \infty$.

Illustrative example: suppose you have a Uniform(0, $\theta$) distribution. If $\theta_{true} < 1$, then for any $\theta \in [\theta_{true}, 1)$, the likelihood function will approach $\infty$. On the other hand, if $\theta_{true} > 1$, then the likelihood will approach 0 for any $\theta$, including $\theta_{true}$.

Cliff AB
  • 20,980