2

I was reading this article on Logistic Regression for Rare Events.

Over here, a modification ("Firth's Correction") to the classical likelihood function has been proposed in which a penalty term has been added based on the square root of the Fisher Information. As we know, the square root of the Fisher Information is closely related to the Jeffreys's Prior:

$$\mathcal{L}(\theta) + \frac{1}{2} \log\left|\mathbf{I}(\beta)\right|$$

I am trying to understand the logic as to why a penalty term was chosen that was based on the Jeffreys's Prior and why exactly it is useful for correcting biases associated with rare events.

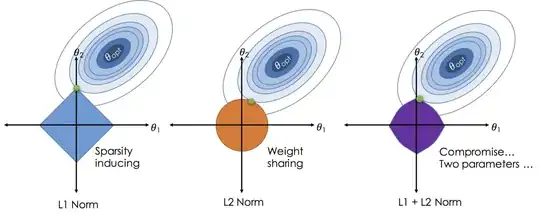
For instance, when it comes to Penalized Regression, I have read about penalty terms based on the L1 Norm and L2 Norms (e.g. LASSO and Ridge). Visually, I can understand why such penalty terms might be useful. The following types of illustrations demonstrate how such penalty terms serve to "push" regression coefficient estimates towards 0 and thereby might be able to mitigate problems associated with overfitting:

enter image description here

However, in the case of Firth's Correction, I am not sure as to how the square root of the Jeffreys's Prior is useful in correcting biases associated with rare events - mathematically speaking, how exactly is a penalty term based on the square root of the Jeffreys's Prior able to reduce biases associated with rare events? Currently, this choice of penalty seems somewhat arbitrary to me and I can't understand how it serves to reduce bias.

Xi'an
  • 105,342
stats_noob
  • 1
  • 3
  • 32
  • 105
  • 3
    As in the tag the prior is named for Harold Jeffreys. Acceptable spellings are Jeffreys prior or Jeffreys’ or Jeffreys’s. – Nick Cox Apr 22 '23 at 06:31
  • 1
    The hyperlink "Logistic Regression for Rare Events" actually links to the paper "Bias Reduction of Maximum Likelihood Estimates". A proper citation would not be amiss to avoid confusion. – dipetkov Apr 22 '23 at 23:17
  • 2
    Found this answer which seems quite relevant: Seeking a Theoretical Understanding of Firth Logistic Regression – dipetkov Apr 24 '23 at 08:06
  • 1
    On a related note -- and I know you've received this advice before -- you'll learn a lot from searching for and reading previous CV threads on topics of interest to you. As an experienced CV user, you of course know how to do this kind of research. – dipetkov Apr 24 '23 at 08:10
  • 1
    @ dipetkov: thank you so much for your reply! This was actually one of the questions I had consulted earlier, but I was looking for more information on this topic. I can include a list of questions I consulted in the reference if you would like. thank you so much! – stats_noob Apr 24 '23 at 14:04

0 Answers0