ZINB vs binomial model goodness of fit testing

Question

I have read that the Vuong test is no longer considered appropriate for testing whether a ZINB fits better than a negative binomial test because it is not strictly non-nested nor partially non-nested. I'm modeling in R (glmmTMB) and there is not the Vuong (nested) option that I can find. If the NB is nested in the ZINB (when ziformula=~0), is it ok to use the Chi-square goodness of fit test? My AIC is considerably lower for the ZINB vs the NB but what is the correct test for the two models? I do have theoretical reasons for why there would be structural zeros.

Answer 1

(Do you really need to do a significance test if the difference in AIC is large and you have a theoretical justification for including zero-inflation? Why?)

tl;dr a parametric bootstrap test is probably the most straightforward solution to your problem; it's moderately computationally intensive (will take something like 2000x the computational effort of fitting your original model, although you could parallelize and might be able to whittle the time down further by using smarter starting parameter values ...)

library(glmmTMB)
m1 <- glmmTMB(count~mined, ziformula =~mined, Salamanders, family="nbinom1")
## fit null/reduced model (no zero-inflation)
m0 <- update(m1, ziformula = ~0)
## parametric bootstrap; simulate data from reduced model, fit with
##   both full and reduced model, find diff(logLik)
simfun <- function() {
    d <- transform(Salamanders, count = simulate(m0)[[1]])
    logLik(update(m1, data = d)) - logLik(update(m0, data = d))) 
}
## simulate a null distribution (SLOW)
set.seed(101); r <- replicate(1000, simfun())
## compute diff(logLik) for real data
obs_diff <- logLik(m1) - logLik(m0)
## compare graphically
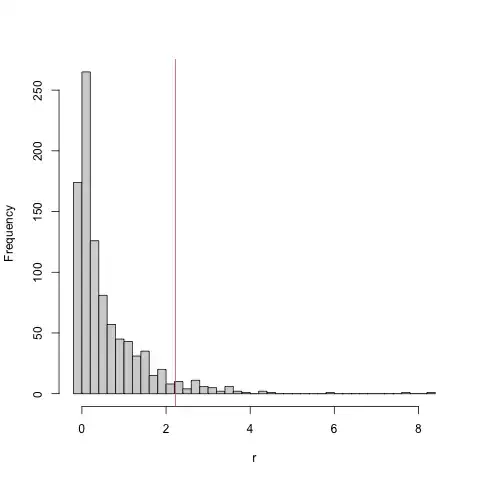
hist(r, breaks = 50); abline(v = obs_diff)
## p-value (proportion that test_stat(null) >= test_stat(observed))
mean(c(na.omit(r), obs_diff) > obs_diff)
[1] 0.05345912

Note there is a minor concern about eliminating NA values (47/1000 in this case) — these are probably cases where the estimated level of zero-inflation converged to 0 ($-\infty$ on the log scale); this will make the p-value slightly conservative.

---

Wilson (2015) goes into detail about why the Vuong test is inappropriate for testing the hypothesis of zero-inflation. For the record they propose some solutions, but none of these are (AFAICS) easily applicable to/available off-the-shelf in your case

Note that when the value of is allowed to be both positive or negative fitted values of do not “pile up” close to zero, and the distribution of zero-modification parameter is normal and hence a non-zero-inflated model is (strictly) nested in its zero-inflated counterpart, and hence a Vuong test for nested models could be used as a test of zero-inflation/deflation. Dietz and Böhning (2000) proposed a link function that allowed for zero-deflation, and more recently Todem et al. (2012) have proposed a score test that incorporates a link function that allows for both zero-inflation and deflation.

As for a "chi-square goodness of fit test": I'm not sure, but I think you mean a likelihood ratio test (whose test statistic, $2 (\log \cal L_\textrm{full} - \log \cal L_\textrm{restricted})$, is $\chi^2$ distributed under the null hypothesis)? This won't work either because it assumes that the null values of the distinguishing parameters (the zero-inflation probability in this case) are not on the edge of their feasible domain. That is, the derivation depends on a quadratic expansion around the null parameter value, and we can't expand around a value of $p_z = 0$ because that would involve negative probabilities ... this issue is mostly thoroughly described for testing the hypothesis that the random-effects variance is zero in a mixed model (see refs in this section of the GLMM FAQ), but the same issue applies here.

Roughly speaking, a likelihood ratio test of significance for a single parameter on the boundary will give a p-value that's twice as large as it should be (again, see refs in GLMM FAQ): this appears to be the case here, where the LRT p-value (from anova(m1, m0)) is 0.1084, very close to twice the parametric bootstrap result.

Wilson, Paul. 2015. “The Misuse of the Vuong Test for Non-Nested Models to Test for Zero-Inflation.” Economics Letters 127 (February): 51–53. https://doi.org/10.1016/j.econlet.2014.12.029.