3

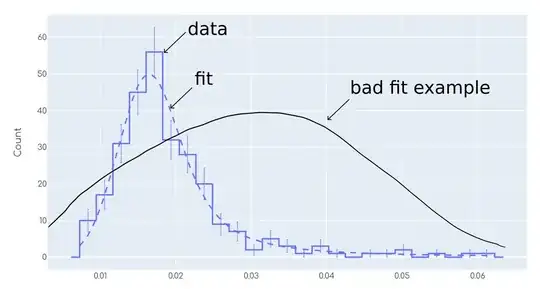
I am fitting a function to data. I want to tell whether the fit is good or not. Consider this example (which is actually my data):

enter image description here

Despite the definition of 'fit is good' being totally ambiguous, most humans will agree in that the fit in the plot is reasonable. On the other hand, the 'bad fit example' shows a case in which most humans will agree in that this fit is not good. As a human, I am capable of performing such 'statistical eye test' to tell whether the fit is good looking at the plot.

Now I want to automate this process, because I have tons of data sets and fits and simply cannot look at each of them individually. I am using a chi squared test, but it seems to be very much sensitive and is always rejecting all the fits, no matter what significance I choose, even though the fits are 'not that bad'. For example a chi square test with a significance of 1e-10 rejected the fit from the plot above, which is not what I want as it looks 'reasonably good' to me.

So my specific question is: What kind of test or procedure is usually done to filter between 'decent fits' and 'bad fits'?

This question is a follow up of this other question.

user171780
  • 229
  • 1
  • 4

1 Answers1

1

The main issue with the chi2 test you are performing is the treatment of empty bins where your estimate of the std is very poor.

Another issue is that the chi2 test assumes normality, but you have counts so theoretically the test won't work. In practice, it might still give you useful answers. If you are able to simulate your data around the best-fit (for example, use the best fit as the expected value for each bin and draw counts from a poisson distribution) then you can base your chi2 test on the simulated distribution instead of the expectation for gaussian data.

Nicolas Busca
  • 171
  • On the contrary, the chi-squared test of counts in binned data does not assume normality. Theoretically, an appropriately constructed chi-squared test will work very well in this circumstance because predictably there are plenty of bins and many of them have sufficiently high expected counts. A bigger issue is that formal testing of distributional fit might not solve the underlying problem: if the choice of distributional shape is ad hoc, the value of the fitting procedure becomes questionable and testing it could have no practical value. – whuber May 12 '23 at 16:49
  • I don't know what you mean by "many of them have sufficiently high expected counts". There are many bins with a only a few counts (1, 2, 3) and, worse, many bins have 0 counts. The test the user refers to compares the chi2 with the number of degrees of freedom assuming chi2 is distributed normally. – Nicolas Busca May 13 '23 at 05:49
  • Those are good points. But (1) when there are many bins you don't need all expected counts to be high (5 or greater) and (2) when you can anticipate there will be tails, you create one bin of each tail in advance to ensure most expected counts will be reasonably large. The fact is that no chi-squared distribution in any contingency table is perfectly chi-squared, but that doesn't matter because the approximation is nevertheless excellent. – whuber May 13 '23 at 15:28