Determine CDF and PDF from quantiles

Question

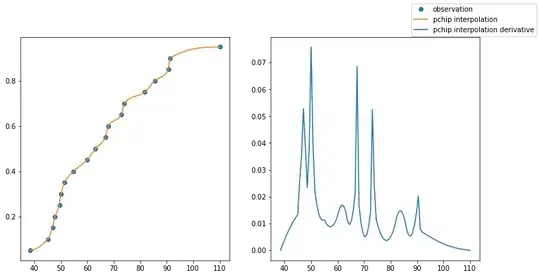
I would like to determine CDF and PDF from quantiles that I have determined via quantile regression. I have read here in the forum (Find the PDF from quantiles) that it is possible to interpolate this via the integral of a B-spline The PDF should then be determined via a normal evaluation. Unfortunately I did not understand why I have to use the integral of the B-spline, how can I ensure that the CDF is monotonically increasing and how I then get to the derivative (the PDF)? Can someone help me please?

This is how it currently looks for me:

import scipy.interpolate
import numpy as np
x = np.array([ 38.45442808,  45.12051933,  46.85565437,  47.84576924,
        49.50084204,  50.09833301,  51.3717386 ,  54.85307741,
        59.91982266,  63.11786854,  66.90037244,  67.84446378,
        72.96120777,  73.92993279,  81.63075081,  85.42178836,
        90.70554533,  91.2393176 , 110.03872988])
y = np.array([0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90, 0.95])
t,c,k = scipy.interpolate.splrep(x, y)
spline = scipy.interpolate.BSpline(t, c, k, extrapolate=False)
d_spline = spline_.derivative()
N = 100
xmin, xmax = x.min(), x.max()
xx = np.linspace(xmin, xmax, N)
fig, ax = plt.subplots(2,1, figsize =(12, 8))
ax[0].plot(x, y, 'bo', label='Original points')
ax[0].plot(xx, spline(xx), 'r', label='BSpline')
ax[1].plot(xx, d_spline(xx), 'c', label='BSpline')

My approach doesn't really work well unfortunately and I can't find any numerical examples to help me. I am grateful for all comments and remarks!

Thank you!

"I have read here in the forum that it is possible to interpolate this via the integral of a B-spline The PDF should then be determined via a normal evaluation." Can you provide a link? — Sycorax, Apr 04 '23 at 13:42
Welcome to CV. The link includes the crucial proviso "with the condition that all B-spline coefficients are nonnegative." Without suggesting a B-spline is a good solution (I think it's not in general), you can find how to create such splines by searching our site for monotonic spline. — whuber, Apr 04 '23 at 13:50
Thank you! I think i find a solution I think I found through your link to a scipy library. https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.pchip_interpolate.html — sdeluxe, Apr 05 '23 at 09:30

score 0 · Answer 1 · answered Apr 05 '23 at 09:35

0

Thank you for pointing this out. I think I have been able to solve the problem for me.

from scipy.interpolate import pchip_interpolate
import numpy as np
x = np.array([ 38.45442808,  45.12051933,  46.85565437,  47.84576924,
        49.50084204,  50.09833301,  51.3717386 ,  54.85307741,
        59.91982266,  63.11786854,  66.90037244,  67.84446378,
        72.96120777,  73.92993279,  81.63075081,  85.42178836,
        90.70554533,  91.2393176 , 110.03872988])
y = np.array([0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90, 0.95])
x_observed = x
y_observed = y
x = np.linspace(min(x_observed), max(x_observed), num=100)
y = pchip_interpolate(x_observed, y_observed, x)
y_d = pchip_interpolate(x_observed, y_observed, x, der=1)
fig, ax = plt.subplots(1,2, figsize=(12,6))
ax[0].plot(x_observed, y_observed, "o", label="observation")
ax[0].plot(x, y, label="pchip interpolation")
ax[1].plot(x, y_d, label="pchip interpolation derivative")
fig.legend()
plt.show()

answered Apr 05 '23 at 09:35

sdeluxe

1

1

Do you trust your own pdf? – Nick Cox Apr 05 '23 at 10:46
1

Continuing the comment by @Nick, that's scarcely a plausible estimate of the pdf. It arises because you are not accounting for the estimation errors in the quantiles. Any reasonable procedure would do so and as a result would definitely not exhibit such extreme spikes -- it would surely result in a far smoother estimated density. – whuber Apr 05 '23 at 16:22
@whuber: If I understood it correctly from the comments, then I would have to account for the estimation errors of the quantiles. Unfortunately, I cannot find a procedure for this. Can you help me with this? Are there any approaches that take this into account? Thank you very much. – sdeluxe Apr 13 '23 at 08:18
See https://stats.stackexchange.com/a/34894/919 or https://stats.stackexchange.com/a/68238/919 for explanations and examples. – whuber Apr 13 '23 at 13:25

Determine CDF and PDF from quantiles

1 Answers1