4

am looking for some advice with some modelling work I'm doing. My data is proportion data which is known to be positively skewed and not normally distributed - histogram below. histogram of data

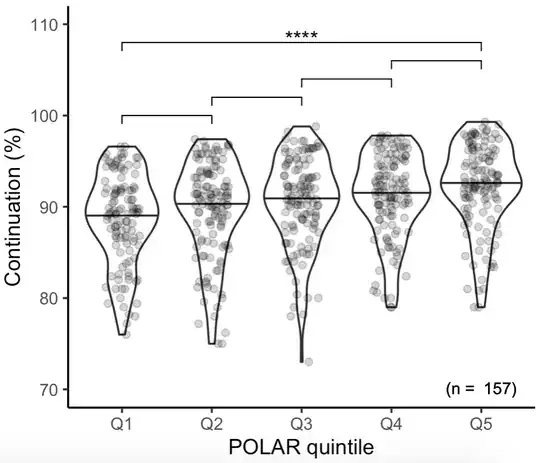
I want to determine the effect of a quintile based metric on this outcome - I know from descriptive plots that it is likely there is a significant effect (see Fig below). Violin plot showing effect of quintile

I'm trying to fit a general linear mixed effect model using lme4 package in R with the following structure. There is pseudoreplication in the dataset at the level of PROVIDER_NAME and YEAR, hence introducing those as random effects.

cont_polar_mod_3 <-glmer(data=ofs2_cont_polar, cbind(Outcome_NUMERATOR, Outcome_DENOMINATOR) ~ QUINTILE + (1 | PROVIDER_NAME) + (1 | YEAR), family=binomial)

However, when I inspect the model using DHARMa, I am unconvinced that I am using the right model structure, as the QQ-plot is a long way off a straight line. The data looks under-dispersed to me, but I'm not entirely sure whether this is relevant for the model structure I am using - think it matters for binomial but not for gaussian (might be wrong here)?

DHARMa plot of model assumptions

Can anyone advise what I should do? Is it safe to use the model as it is even though the QQplot looks bad, or do I need another structure? For reference I've tried adding with and without an observation level effect term, and have tried using both a calculated proportion column and cbind column as my response variable. I've also tried log transforming the response variable. None of which changes the QQplot very much.

With thanks in advance, Katharine

[Update 1] - Apologies, realise I set up my cbind column incorrectly. Have now set it up as cbind(success, failure) not cbind(success, total) and get the following plots in DHARMa which look better?

revised DHARMa plots

[Update 2] Have now tried modelling with a beta distribution as per @ShawnHemelstrand suggestion, with the revised cbind column. This looks better? revised DHARMa plots with beta distribution

KatharineH
  • 41
  • The plots do look slightly concerning, but I'm more curious about why you modeled this as a binomial family regression. Given it is left-skewed, shouldn't you use a different family like a beta distribution? – Shawn Hemelstrand Mar 26 '23 at 03:25
  • Binning a continuous variable entails loss of information. It also makes the implicit assumption the relationship between predictor and outcome is the same for all observations that happen to be in the same bin. Do you have the original measurements of POLAR? More on this topic: What is the benefit of breaking up a continuous predictor variable?. – dipetkov Mar 26 '23 at 13:28
  • 1
    @dipetkov Agree that I would ideally not use a quintile based system and use the raw continuous data, but am using a publicly available dataset that only contains the quintiles and not the original measurements. – KatharineH Mar 26 '23 at 16:25
  • Thanks @ShawnHemelstrand - will confess am reaching the limits of my statistical knowledge. Have tried a beta distribution in Update 2 which looks a lot better? Would you think that QQplot was good enough now? – KatharineH Mar 26 '23 at 16:42
  • I would say these plots have much less egregious departures from normality. What do your quantile-based tests look like? Have you met all of the assumptions for fitting a GLMM (linearity, no multicollinearity among predictors, etc.)? – Shawn Hemelstrand Mar 26 '23 at 19:30

0 Answers0