3

I am currently at a dilemma concerning a model describing the allometric relationship between body size and mass. After carefully checking model assumptions and selecting the model that best fits the data, my final model was the following :

modD=lmer(body_size~0+(D_Mass*Species*sex+D_Mass*sex*Season +Species*Season)+(1|site), data=Rhabdoglobal, REML= T)

Diagnostic plots showed no indication of non-linearity or violating the normality of residuals or heteroscedasticity of variances. 0 was chosen for the intercept as biologically we know for a fact that at 0 body size there is 0 mass, so the relationship between the two must always cross the point (0,0). These were the results of the Anova :

Type III Analysis of Variance Table with Satterthwaite's method

           Sum Sq Mean Sq NumDF  DenDF  F value    Pr(>F)   




D_Mass             214.78 214.782     1 676.03 717.7672 < 2.2e-16 ***


Species            510.73 255.365     2 120.41 853.3874 < 2.2e-16 ***
sex                  0.95   0.950     1 678.15   3.1732 0.0753052 .

Saison               8.71   8.706     1 680.00  29.0926 9.533e-08 ***
D_Mass:Species       0.01   0.007     1 678.49   0.0231 0.8791882

D_Mass:sex           0.01   0.014     1 677.11   0.0456 0.8308968

Species:sex          0.96   0.964     1 677.12   3.2204 0.0731712 .

D_Mass:Saison        7.02   7.017     1 677.22  23.4497 1.590e-06 ***
sex:Saison           3.90   3.904     1 676.44  13.0453 0.0003265 ***
Species:Saison       0.26   0.257     1 562.45   0.8579 0.3547159

D_Mass:Species:sex   1.08   1.082     1 676.27   3.6148 0.0576921 .

D_Mass:sex:Saison    3.59   3.590     1 675.85  11.9973 0.0005664 ***

However, when I try to illustrate my results in plot form, the relationship does not seem linear at all. enter image description here

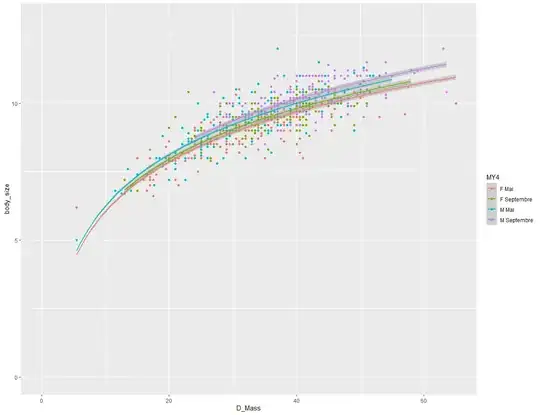
Rather, changing the plot expression to y=log(x) seems to solve that problem : enter image description here

My questions would be the following :

  1. Is it possible to represent a relationship that was described by a statistical model using a different expression than if one would draw a plot directly from the model estimates ?
  2. If not, is it justifiable to use a different model, not necessarily better in terms of linearity, homoscedasticity or normality of residuals, but simply based on post-hoc representation of raw data ?

Edit : thank you for the response. Using a backward stepwise method,this is the simplest model with the lowest AIC that I came up with.

Shawn Hemelstrand
  • 13,543
Hake98
  • 31
  • 2
    I would strongly recommend you start with a MUCH simpler model so that you can understand it well and diagnose problems. – mkt Mar 20 '23 at 20:24
  • 3
    Why do you believe the fit must pass through (0,0)? Check it out with the simplest model you can imagine and a small set of synthetic data. Use a categorical explanatory variable. – whuber Mar 20 '23 at 20:26
  • 3
    Relationships such as these are most often explored on a log-log scale, and there is a substantial literature about this too. I would start with just examining log(mass) as a function of log(size). – mkt Mar 20 '23 at 21:45
  • 3
    Stepwise methods are terrible: https://stats.stackexchange.com/questions/20836/algorithms-for-automatic-model-selection – mkt Mar 21 '23 at 08:20
  • 3
    Your plotted data are inconsistent with a straight line passing through the origin. The problem thus has to do with your model itself, which nevertheless attempted to force a straight line through the origin. I suspect that the large number of interaction terms allowed the model to work around that unrealistic constraint for the observed mass values on the order of 20 to 50, but extrapolation down to 0 mass is unrealistic. – EdM Mar 21 '23 at 16:54

1 Answers1

3

I assume that by 'size', you mean something like body length.

Your model is inconsistent with the data, and ignores much that is known about such scaling relationships in biology. As a start, it's worth modelling both size and mass on a logarithmic scale, because these relationships exhibit power laws.

Secondly, that is a remarkably complex model, given what is known about these allometric relationships. If analysed properly, I would be very surprised if you found that many of those terms had a strong influence on the size-mass relationship.

Thirdly, you're also being led astray by your use of stepwise selection methods to do statistical inference. As explained well in this thread, stepwise selection leads to heavily biased results and there are always better ways of analysing data.

Finally, I would also recommend writing your code differently. As written, you have multiple redundant main effects and interactions. R interprets this intelligently and filters out the duplicate terms, but it's not good practice and is liable to lead to confusion.

mkt
  • 18,245
  • 11
  • 73
  • 172