2

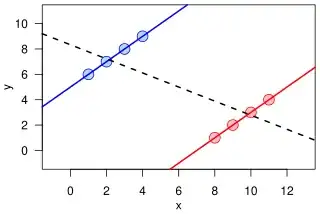
I have a data set with a continuous LHS variable y, continuous RHS variable x, and a dummy D. I am running two OLS regressions: $$y_i=\beta_0+\beta_1*x_i+\epsilon_i$$ and $$y_i=\gamma_0+\gamma_1*x_i*(D_i=1)+\gamma_2*x_i*(D_i=0)+\eta_i$$ My estimated $\hat{\beta_1}$ coefficient is larger than both $\hat{\gamma_1}$ and $\hat{\gamma_2}$, which confuses me. Shouldn't it be the weighted average of the two sample-specific slopes (with positive weights)? The regression samples do not change.

With the Stata code below, I can replicate the result, but I don't have a good intuition of what is happening:

clear all
set seed 1234
set obs 10000
gen x=runiform(0,100)
gen d=x>50

gen y=2-5x+rnormal(0,1) if d==0
replace y=2-2x+rnormal(0,1) if d==1


reg y x
predict y_pool
reg y c.x#i.d
predict y_int 
twoway (scatter y x if d==0) (scatter y x if d==1) (scatter y_pool x, color(green)) (scatter y_int x, color(orange)), legend(order(1 "D=0 sample observations" 2 "D=1 sample observations" 3 "Pooled predicted values" 4 "Sample-specific predicted values"))
lippi
  • 23
  • You do indeed have a common intercept for both groups in the second regression? – Christoph Hanck Mar 20 '23 at 12:22
  • Hi Christoph, thank you for writing. Yes the intercept is the same. I have now added a code to replicate the result to the original question. – lippi Mar 20 '23 at 12:28

1 Answers1

1

Shouldn't it be the weighted average of the two sample-specific slopes (with positive weights)?

First of all, you are not calculating weighted average there. Your second model calculates separate slope for each group, the first one, single slope for all the samples. You are not calculating the weighted average anywhere, at least this is not what you are showing.

Second, answering your question, no they shouldn't in the case described by you. On example where this does not happen is Simpson's paradox. You can have completely different slopes for groups and for all the data. One such a case is shown below, where each group has a positive slope, but the overall slope is negative.

Simpson's paradox diagram from Wikipedia

If you indeed calculated separate models per each group and calculated weighted average of the slopes, than, as a convex combination, the result would fall somewhere between the two original slopes.

Tim
  • 138,066
  • Thank you very much Tim. Yes, I was aware of the Simpson's paradox, but I believed that we need to include separate intercepts to estimate a pooled coefficients that is outside the sample-specific estimates. This was then a mistaken intuition. – lippi Mar 20 '23 at 12:33
  • Could you please explain a bit more what do you mean by this: "First of all, you are not calculating weighted average there. Your second model calculates separate slope for each group, the first one, single slope for all the samples. You are not calculating the weighted average anywhere, at least this is not what you are showing." What would be a set-up that calculates the weighted average? – lippi Mar 20 '23 at 12:35
  • @lippi are you calculating weighted average? If yes, you didn't describe it. How is it related to the second model? – Tim Mar 20 '23 at 12:36
  • I think I may not understand clearly what you mean by that. Could you please take a look at the code added to the original question? Thank you. – lippi Mar 20 '23 at 12:39
  • @lippi I am not a Stata user, but you seem to be fitting a regression model with an interaction term. The code does not seem to be calculating any weighted average anywhere. You also are calculating a single model, rather than two models and averaging their parameters. – Tim Mar 20 '23 at 12:41
  • Okay, thank you! – lippi Mar 20 '23 at 12:49