0

Suppose we have a set A , we split into multiple disjoint subsets ai We only have access to the ai sets , is there a way to compute the ECDF for the set A without looking at it ? If for example we have ECDFi on ai and we average them , do we have guaranteed convergence ? We can not just combine all the subsamples for memory issues , the only thing we can do is compute the ECDF for each subsample so instead of k samples for the subset ai we will have 100 values ,(ECDF evaluated at 0% 1% .. 100%) which reduces drastically the memory needed , a subset can have a size of 1000000 , we compress everything into 100 digits Now given these 100 digits for each subsets how to infer the ECDF for the A which is the union of the ais

By average here I mean vertically (if we stack the ECDFs vertically) FA(0%) would be avg(Fai(0%) and so on for each X%

I actually did some simulations to find out and it seems that it works

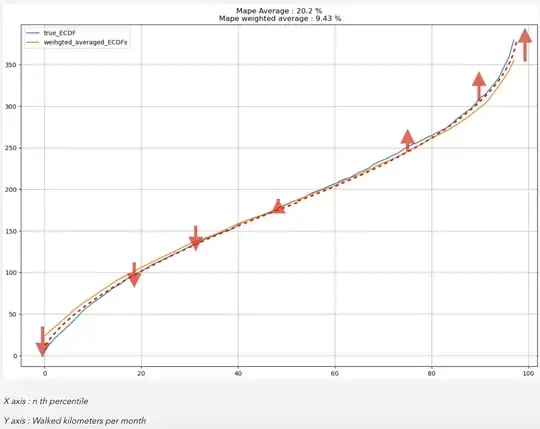
I’ve chosen this metric (mape) because in case of the ECDF , the 100% percentile is by definition the largest , therefore an error in the 100% percentile would inflate the whole error , even though it is an error in only one point of the function . For example an error on the 100% percentile of approx: 400 vs true : 800 , we want it to be treated the same way as an error of approx : 40 vs true : 80 in the 40% percentile , because we want the function to converge in each point , we may even tolerate divergence in the 100% percentile.

enter image description here

  • avg_mape is the average error when we only averaged the ECDFs
  • weighted_avg_mape is the average error when we averaged using weights that are proportional to the size of the subset ai the ECDFs

I tried different underlying distributions with different parameters (sigma , mu , lambda ..) The imbalance here refers to how uneven the partitioning is doen (A to ais) you can see it as inversely proportional to the entropy , with max entropy all ratios are even and lowest entropy something like 90% , 1 % 9 %

But we know already that the average will dilute the 100% percentile (we average the true 100% with inferior factors ) and will inflate the minimum . Nearby percentiles will have similar behavior as well , as shown in this figure :

enter image description here

What we would like to do is to bend the curve a little from the extremities (up in the right and down in the left )

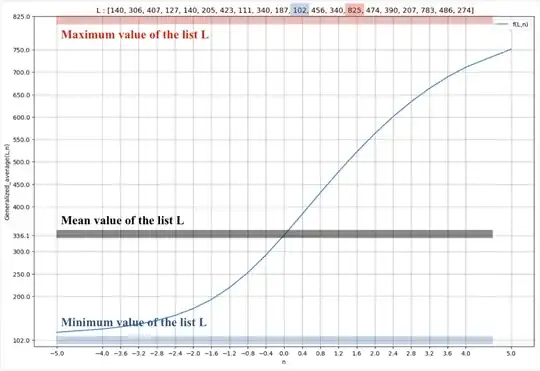
I came up with the following function to do it (kind of a generalized formula for the average ) :

$$F( L , n) = \sum (li^{n+1})/\sum (li^n)$$

L : List of positive numbers

if n goes to ∞ F returns the maximum of L if n goes to -∞ F returns the minimum of L if n = 0 F returns the average of the list L

Here is how the function acts on a list while varying the n

enter image description here

We can of course use the weights coming from the size of subsets ai combined

And now instead of using a weighted average vertically we will use F(Lx% , n) L x% is the list containing all the Fai(10%) for example n would tend toward infinity if X is 100 toward -∞ if X is 0% 0 if X is 50% and for the rest of the values we will vary n the n continuously from -∞ to +∞

Here is an example of the result after bending the extremities

enter image description here

Following is the evaluation of different approaches :

enter image description here

Now the problem is that I can not come with a consistent proof of the convergence of the approach even-though it sounds intuitive ? And I really have no Idea how accurate all of this is ?

User1865345
  • 8,202
Amine boujida
  • 15
  • 2
    Because the collection of ECDFs of the subsets is equivalent to the ECDF for the entire set, could you please explain what you mean by "not looking at it"? Precisely what information do you wish to ignore and why? Note that the abstract problem you state, of relating the ECDFs of the subsets to the entire set, is not generally soluble because it depends on how the subsets are chosen, which you don't seem to specify. – whuber Mar 03 '23 at 21:15
  • The subsets are created randomly , we will sample without replacement many times until wa have n set ai , if for instance card(A)= 20, a1 would have 2 then a2 would have 14 , and a3 would have 4 Now we are only allowed to compute the ECDF on the ais given ECDF1 (computed on a1) and ECDF 2 and ECDF3 We want to study the vertical average of the ECDFs (vertical means the 1% percentile is the average of 1% from ECDF1 and ECDF 2 and ECDF3 , and so on for all X%) – Amine boujida Mar 04 '23 at 00:13
  • Computing the ECDF on 10 % for A for instance means we need to rank the date and take the first 10% and take themaximum value But we can not do this since we do not have access to A So instead we do it on the ai subsets how can we reconstruct the ECDF of A given the ECDFs on ai – Amine boujida Mar 04 '23 at 00:16
  • 3
    I'm not sure I follow, but it sounds like you have multiple independent random samples from a population. If so, the combined ECDF is your best estimate of the parent distribution (according to laws of large numbers). I cannot determine what you might mean by "not have access to," because either you have these subsample ECDFs--in which case there's nothing stopping you from combining them, which is an easy and efficient computation (any ECDF is equivalent to a sorted dataset)--or you don't, in which case it's unclear what you do have. – whuber Mar 04 '23 at 00:18
  • We only have access to the ECDF of each subsample ai - We do not have access to the actual samples We know that A = Union of ais We want to compute the ECDF for A What do you mean by the combined ECDF please ? – Amine boujida Mar 04 '23 at 01:43
  • 3
    If you have access to an ECDF, it is equivalent to getting the ordered sample. – Xi'an Mar 04 '23 at 10:06
  • Following up on the previous comments about ECDFs being equivalent to ordered samples, note that the ECDF of the union of those samples is the (point by point) arithmetic mean of the ECDFs, weighted by the subsample sizes. Thus, with a simple averaging algorithm if you have "access to" the subsample ECDFs and you know their sample sizes, you have the ECDF of the union of all the samples. That leads to a direct, simple convergence argument. – whuber Mar 04 '23 at 13:18
  • But how you prove the convergence mathematically , I know that It works intuitively , but using a consistent proof , because we know that in the extremities the convergence goes such as the true F(100%) is the sup of the averaged 100% , the opposite behavior for the 0% The work I did was an empirical way of seing things , I'm looking for a direct proof , that will help generalizing on many cases , understand why in the case of normal the error is different from exponential , what space to choose for the n (the bending parameter) according to each distribution . and so on .. Thank you – Amine boujida Mar 05 '23 at 17:28
  • We can not combine the subsamples that is the constraint , it could be for memory problem , combining them would result in memory error , so what we can do is compute ecdf for each and then infer the true ECDF based on the computed ecdf for subsamples Fitting all the samples into memory and then computing the ECDF is nt working in this scenario – Amine boujida Mar 05 '23 at 17:30
  • 2
    @Amineboujida but you don't need to put them into memory, you only need to sort and count them, neither need to keep them in RAM. Also, you can put quite a lot of floating-point numbers in the memory of an average modern-day computer. Could you clarify what exactly is the problem you are trying to solve? – Tim Mar 05 '23 at 17:56
  • I have added MathJax for better formatting @Amineboujida. If there is anything wrong, please edit it. – User1865345 Mar 05 '23 at 17:57
  • 2
    If RAM is a problem, then any of the solutions at https://stats.stackexchange.com/questions/35220 will address that. Back in the days when RAM was limited (1950's) and data access was slow and serial (think tape drives), people developed ingenious efficient methods to combine datasets using almost no RAM, such as Merge Sort. It's doubtful you would need such a solution. These computing issues are unrelated to the convergence question, which (as I mentioned) is straightforward, because a set of independent random samples is a random sample. – whuber Mar 05 '23 at 19:05
  • I mentioned the RAM issue just to illustrate it, the problem is simple , Does the average of the ECDFi converges toward to ECDF on the whole sample , if so , how can we demonstrate it , and is the rate of convergence predictable . When I say proof I mean this kind of proofs (Glivenko–Cantelli theorem) : https://en.wikipedia.org/wiki/Empirical_distribution_function @Tim , could you elaborate what you mean by sort and count set thresholds in prior like [10 , 50 , 300 .., ti ] ? each subsample would return lists like that shows the count of values <ti then we sum everything ? – Amine boujida Mar 05 '23 at 19:33
  • A complete proof has already appeared in my comments. It requires the average to be weighted. If it is not weighted, then the proof is more delicate. But why would you not use the proper weighting for the averaging in the first place? – whuber Mar 06 '23 at 14:59

0 Answers0