I am working on my bachelor thesis with time series data. The idea is to predict the expected battery life based on voltage data from sensors.
During my research I came across SARIMAX. For me this ML algorithm sounded very plausible at first. Unfortunately, I was only able to generate constant predictions. Since I was not sure if this prediction was due to the underlying possibly incomplete data set. I Calculated a data set with charge and discharge curves myself.
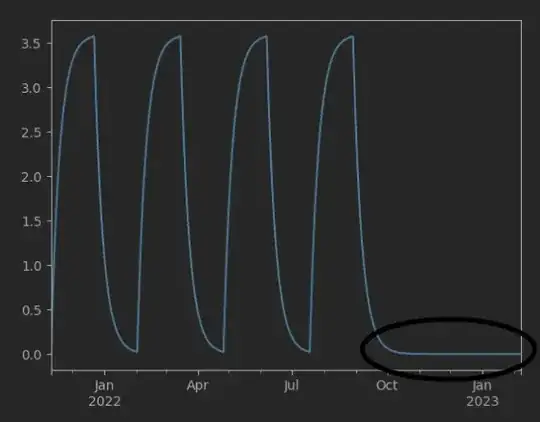
So the data set my questions refer to looks like this:
Before passing the data to the algeorithm for learning, I logarithmized the data, formed the firstdifference, and tried to clean up the difference in seasonality. When I create a prediction with SARAMIAX I get only one constant like here:
My goal is to continue writing the curve into the future something like this:
I have read in some examples that it is not an error of the Sarimax model, but since the prediction only refers to the previous value, only a constant can be predicted.
Now, of course, I'm wondering whether I'm on the wrong track with SARIMAX, or whether I've simply taught the model incorrectly and can continue to work with SARIMAX. Maybe there is another ML algorithm you would prefer for this task?
Maybe someone reads this post who has experience with the prediction of time series data and puts me back on the right track.
I appreciate any kind of feedback, thank you in advance.
Edit:
The original data is transmitted by the sensors every 15 min, I resampled the data over the average to 1H. The data of a sensor look for example as follows:
Since the original data have different periods and I'm not sure how to deal with it, I first created the data set with uniform periods for simplicity. The self-generated data are recorded hourly, whereby a charge-discharge cycle lasts 2000 hours.
I attach the class with which I create the data, maybe this is the easiest way to explain myself.
class CapacitorCurve:
C = 1 # Kapazität des Kondensators in Farad
V0 = 3.6 # Anfangsspannung des Kondensators in Volt
R = 1 # Widerstand des Stromkreises in Ohm
tau = R * C # Zeitkonstante in Sekunden
t = np.linspace(0, 5 * tau, 1000)
def init(self, C=1, V0=3.6, R=1):
self.C = C
self.V0 = V0
self.R = R
Funktion zur Berechnung der Ladekurve
def capacitor_charge(self, t, tau, V0):
return V0 * (1 - np.exp(-t / tau))
Funktion zur Berechnung der Entladekurve
def capacitor_discharge(self, t, tau, max_capacity):
return max_capacity * np.exp(-t / tau)
def multiple_charging_cycles(self, cycles):
counter = 1
max_capacity = 0
min_capacity = 0
charging_cycles = np.empty(shape=1)
for i in range(cycles):
if counter == 1:
charging_cycles = self.capacitor_charge(self.t, self.tau, self.V0)
max_capacity = max(charging_cycles)
counter += 1
else:
charging_cycles = np.concatenate(
(charging_cycles,
self.capacitor_charge(np.linspace(min_capacity, 5 * self.tau, 1000), self.tau, self.V0)))
counter += 1
charging_cycles = np.concatenate(
(charging_cycles, self.capacitor_discharge(self.t, self.tau, max_capacity)))
min_capacity = min(self.capacitor_discharge(self.t, self.tau, max_capacity))
return charging_cycles
To Dataframe:
cc = CapacitorCurve()
spannungskurven = cc.multiple_charging_cycles(5)
df = pd.DataFrame(spannungskurven)
noise = 0.03 * np.random.normal(size=spannungskurven.shape)
spannungskurven_noise = spannungskurven + noise
df['spannungskurven_noise'] = spannungskurven_noise
df['spannungskurven'] = pd.DataFrame(df[0])
my_date_range = pd.date_range(end='2023-01-01', periods=len(df), freq='H')
df['DateTime'] = my_date_range
df.set_index('DateTime', inplace=True)
df.index.freq = 'H'
df.replace([np.inf, -np.inf], np.nan, inplace=True)
df = df.dropna()
df = df.drop(columns=0)