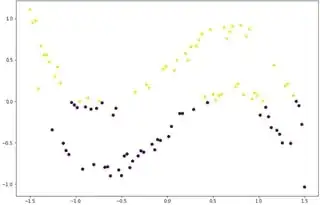
Assume the following data, where the yellow points represent class $1$ and the purple points represent class $2$. I would like to know, if it is possible to build a linear classifier (sigmoid) by transforming the data accordingly?
To get some intuition for the log loss in combination with the sigmoid function, I have tried to classify the data by adding only $1$ dimension for the bias.
Data :
func = lambda x: np.sin(x) - 0.5 * x ** 3
x1 = np.linspace(-1.5, 1.5, 100)
class1 = np.random.uniform(0.5, 1, size = 50) * 0.5
class2 = np.random.uniform(-1, -0.5, size = 50) * 0.5
class_concat = np.concatenate([class1, class2])
np.random.shuffle(x1)
np.random.shuffle(class_concat)
x2 = func(x1) + class_concat
x3 = np.ones(len(x2))
x = np.vstack([x1, x2, x3]).T
y = np.array([0 if val < 0 else 1 for val in x[:, 1]])
Model:
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def log_loss(pred, label):
return - np.sum((label * np.log(pred)) + (1-label) * (np.log(1 - pred))) / 100
w = np.random.uniform(-0.1, 0.1, size=(3, 1))
num_epochs, lr = 500, 0.004
for _ in range(num_epochs):
z = x @ w
pred = sigmoid(z)
loss = log_loss(pred, y)
grad = -(1/100) * x.T @ (sigmoid(z) - y[:, None]) #
w = w - lr * grad
print(f'loss after {_+1} epochs: {loss}')
As expected, using $3$ weights, ($1$ bias), I do not get good seperation:
My idea was now, to transform the data, for example by expanding it to some polynomial, and thus using more weights:
$ X = w_0 + w_1x + w_2x^2 + w_3x^3 .... w_{n}x^n$. In theory, I intuitively think this could work, since I allow the model a lot of flexibility for each weight to minimize the loss, but it seems hard to optimize the loss function using gradient descent. I would appreciate any input that could guide me in the right direction!