Sanity checking survival model

Question

I have some basic statistics foundations (Lean Six Sigma, Industrial Engineering in College), but I'm completely new to survival analysis, and relatively new to Data Science. So I'm looking to sanity-check my reasoning and whether my interpretation of the results is good.

Some context:

I've got a large survival dataset for employee turnover, numerous features (mostly psychometric), and I am looking to build a classifier to identify candidates that are likely to have a long tenure vs. those who would not.

Using Orange Data Mining. I continuized, standardized and imputed missing data before feeding it into a regularized cox regression. With fine-tuning of the regularization and feature selection, including a couple interactions, I got a C-index just under 0.7.

I then created a categorical target to distinguish between successful and non-successful candidates, using a cut-off survival time. I fed the cox risk score along with some of the original features into a logistic regression and managed to get an AUC of just over 0.7.

Finally, I tweaked the classification threshold using a calibration plot to balance precision, recall and proportion of selected candidates. The prediction using this threshold would be my model's end result, giving a "high risk" and a "low risk" binary classification.

I am currently looking into justice algorithms for pre-processing, to avoid any bias in the model disproportionately affecting certain groups.

The questions:

1. On model performance: I know that an r-value of 0.95 for linear regression is generally considered good in engineering. I have also heard that in psychology and sociology, the tends to be way lower due to the complexity of human behavior, but I am not informed on what a good rule-of-thumb value is for such scenarios.
   I also don't know what a good standard is for C-Index and have based my evaluation of the model solely on its definition (0.5 = useless, 1 = perfect, 0.7 = decent??)

   What is a good target for this metrics?

2. On Kaplan-Meier Plots: First thing I did was to 70-30 split my data into training and validation sets. If I classify and graph both sets on the same graph, I get the following curves: 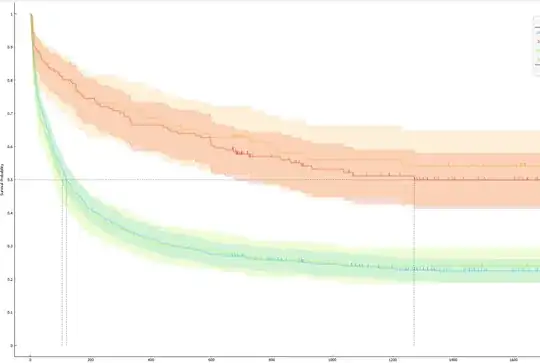From which I interpret:

   A) Since the "high risk" and "low risk" survival curves differ, and their confidence intervals do not overlap, I can be confident that the classification model accurately distinguishes between candidates likely to have a long tenure and those likely to have a short one.

   B) Since the confidence intervals for the testing and validation sets overlap, I can be confident that this model can make useful predictions on unseen data, assuming.

   Am I interpreting this correctly?

Thanks in advance for any advice,

Answer 1

A few things to consider.

If you have more than 20,000 cases or so, then your train/test split could make sense. I can see individual steps in the plotted survival curves, however, so I doubt that you have quite that many. If you don't, you run a risk of losing precision in training the model and sensitivity in testing. See Frank Harrell's post on the subject.

It looks like you did a single imputation of missing values. That doesn't take into account the imprecision in doing the imputations. Best practice is to do multiple imputations and summarize results in a way that takes the variance introduced by imputation into account. See Stef van Buuren's Flexible Imputation of Missing Data.

The C-index is OK for evaluating a particular model, but it's not very sensitive for comparing models. It's only a measure of discrimination, not of calibration. See this answer and its comments. There is no rule-of-thumb for a "good" C-index in survival analysis. More important: from your business perspective, how much discrimination do you need among employees? Is what you have accomplished adequate for that business purpose?

It's not clear what you gained by converting from a survival model's risk score to a binomial regression, particularly when you re-introduced predictors from the survival model into the binomial regression. I fear that the apparent improvement in C-index you found might just be over-fitting your current data. Then the dichotomization into "high risk" and "low risk" groups throws away a lot of potentially useful detailed information about the probability of job turnover over time.

The Kaplan-Meier plots show that around time = 1500, ~25% of your "high risk" group is still employed, which is a reasonably large percentage, versus ~50% of your "low risk" group. Is that difference really so important from a business perspective, particularly when the dichotomization is throwing away a lot of information about intermediate probabilities of survival?

The best way to estimate the performance of the model on new data would be to demonstrate the calibration of observed versus predicted survival probabilities at one or more time points of interest. If you do have a very large data set, then you can do that by train/test split. Otherwise, you can do that via bootstrapping. You repeat all of the model-building steps on each of multiple bootstrap samples and then compare performance of each resulting model on its corresponding bootstrapped sample and on the total data set.

Frank Harrell's rms package in R provides tools for all of the above: imputation, survival modeling, and model validation and calibration. His Regression Modeling Strategies course goes into extensive detail on the matters touched on above.