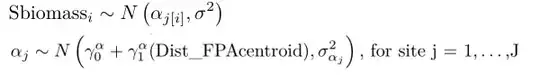1

I wanted to write the mathematical equation for my model below. It is a glm that tries to explain the relationship between the sum of observed biomass of several replicas at different observation sites as a function of distance from a given point, plus the random effect of the sites. I also use the Gamma family. I used the extract_eq function of the equatiomatic package to obtain the mathematical equation of my model but I am not sure of the result obtained...

library(equatiomatic)
library(lme4)

mod <- glmer(Sbiomass ~ Dist_FPAcentroid + (1|site),family = Gamma(link = "log"),data =my_data)


extract_eq(mod)




$$
\begin{aligned}


\alpha_{j}  &amp;\sim N \left(\gamma_{0}^{\alpha} + \gamma_{1}^{\alpha}(\operatorname{Dist\_FPAcentroid}), \sigma^2_{\alpha_{j}} \right)
\text{, for site j = 1,} \dots \text{,J}



\end{aligned}
$$

When I knit this result in RMarkdown, it doesn't work because of the line break between the first and second line. If I remove this line break I get this :

enter image description here

However, it seems to me that this equation is not complete and is missing a part. Should it look more like the equation below or have I misunderstood ?

enter image description here

Thank you in advance for your reply

COOLSerdash
  • 30,198
Florian B.
  • 87
  • 1
    That doesn't look right to me: You specify a gamma distribution as your conditional distribution but the equation assumes a normal distribution. – COOLSerdash Dec 19 '22 at 08:49
  • Thanks for you answer @COOLSerdash. How would you write this equation correctly ? – Florian B. Dec 19 '22 at 08:53

1 Answers1

2

You're fitting a conditional Gamma distribution with a log-link to the data. As such, the equations would be: $$ \texttt{Sbiomass}_{ij}\sim \operatorname{Gamma}(\mu_{ij}, \phi) $$ where $\phi$ is the shape (assumed constant) and $\mu_{ij}$ is the conditional mean: $$ \operatorname{E}(\texttt{Sbiomass}_{ij}\,|\,\texttt{Dist_FPAcentroid}_{ij}, \texttt{site}_{ij}) = \mu_{ij} = \exp(\beta_{0,j} + \beta_1\texttt{Dist_FPAcentroid}_{ij})\quad \text{for site} \;j=1, \ldots, J $$

with the random intercept assumed being drawn from a normal distribution: $$ \beta_{0,j} \sim \operatorname{N}(0, \sigma^2_{\beta_0}) $$

See also https://stats.stackexchange.com/a/126225/21054 and https://stats.stackexchange.com/a/431272/21054

COOLSerdash
  • 30,198