0

I have an empirical observation with about 300K continuous values. I fitted these values (with disfit python library) getting a loggamma distribution: 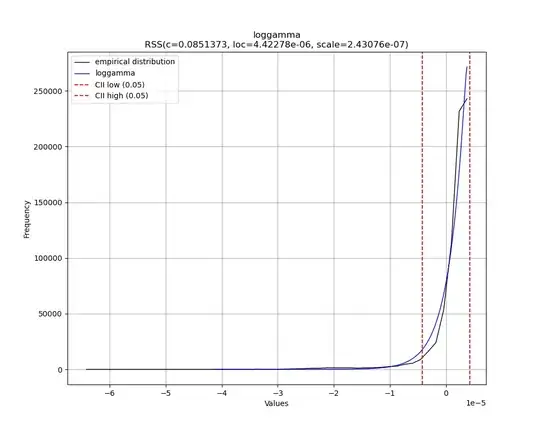enter image description here The resulting parameters are:

  • c = 0.08513733275923194
  • loc = 4.422783357274778e-06
  • scale = 2.430755669784885e-07

I want to estimate the probability of observing certain values of $x$, then so I coded a proof-of-concept:

>>> from scipy.stats import loggamma

>>> c = 0.08513733275923194
>>> loc = 4.422783357274778e-06
>>> scale = 2.430755669784885e-07


>>> x= -0.000001


>>> print( loggamma.pdf(x, c, loc, scale) )
>>> print( loggamma.cdf(x, c, loc, scale) )


54747.465342747964
0.1563094678919458

If my interest is to estimate the probability of $x$, what should be the interpretation of the results of the above? I mean, for the cdf, I understand that the result near $0.16$ is the probability of having a value equal to or less than $x=-0.000001$. However, does not make sense to me the result of the pdf does. If the result is a frequency value, should I divide it by the sample size? Sorry, I'm not a statistician.

Fernando Barraza
  • 25
  • Why are you fitting a distribution at all? With so much data, why not just use their empirical distribution? – whuber Dec 07 '22 at 20:22
  • @whuber It's possible? I just only need to get the probability of $x$ but I don't know how to deal with when such $x$ value isn't in my data, so I figure that if I know what distribution my data follows then I can calculate it. – Fernando Barraza Dec 08 '22 at 17:31
  • The empirical distribution is the distribution exhibited by your data. See https://stats.stackexchange.com/search?q=empirical+distribution+function+ecdf for relevant posts and illustrations. – whuber Dec 08 '22 at 17:58
  • Thanks, @whuber! I just encoded the ecdf of my sample data and got good results, very close to the theoretical loggamma distribution. Just to know, in my post, what does the $54747.465342747964$ result of the pdf calculation mean for $x=-0.000001$? I expected a value between $0$ and $1$ – Fernando Barraza Dec 08 '22 at 19:48
  • https://stats.stackexchange.com/questions/4220 – whuber Dec 09 '22 at 14:51

0 Answers0