How to found the bound $M$ in rejection sampling when the differentiation of the ratio of target and proposal density is not possible?

Question

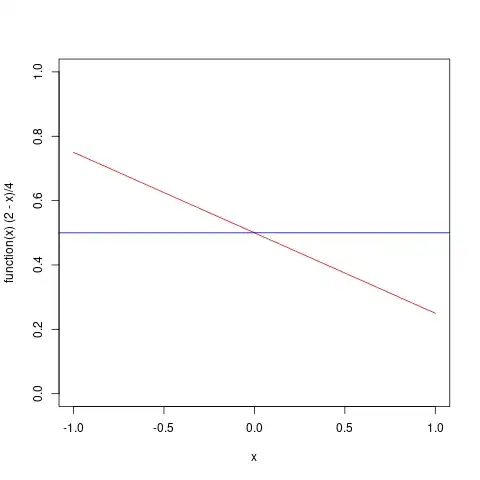
Suppose we have the following PDF of X:

$f(x)=\frac{1}{4}(2-x)\;;-1\leq x\leq 1$

We want to use $g(x)\sim\mathrm{Unif}(-1,1)$ as a proposal density to generate samples from $f(x)$ using a rejection sampling.

Our usual approach will be, to find $M$ such that

$M=Sup_{x\in [-1,1]}\frac{f(x)}{g(x)}$

But we can not calculate it by differentiating $\Phi=\frac{f(x)}{g(x)}$ with respect to $x$ and equating it to 0.

Are there any other possible ways to find the upper bound?

I don't see why not. This derivative check is part of an examination of critical points. It will establish that the only critical points are $\pm 1,$ which both constitute the boundary of the domain of the ratio as well as being where the ratio is not differentiable. — whuber, Dec 07 '22 at 04:18

score 1 · Answer 1 · answered Dec 06 '22 at 21:25

Hint: did you try to plot this density functions? Both are linear functions (on the range $[-1, 1]$) so there is no need for calculus.

So just calculate, with a view on the above plot, $$M = \sup_{x\in [-1,1]} \frac{f(x)}{g(x)} = 2\cdot \sup_{x\in [-1,1]} = 2\cdot \frac34 $$

1 Answers1