What is an effective way to visually compare many sets of confidence intervals?

Question

I am trying to compare intervals for two sets of data. I have $N$ pairs of intervals, where each pair has an interval corresponding to treatment $A$ and then treatment $B$. For example, in the $i$-th pair, I have

$$ (CI^{A}_i, CI^{B}_i) $$

I would like to compare these visually. An idea that comes to find is a type of crosshair plot, where it looks like

$A$ can be in the x-axis, while $B$ in the y-axis. Is there a more effective way to compare sets of intervals? I am mainly interested in whether intervals overlap in general.

Overlap of confidence intervals isn't a good way to evaluate statistical significance, if that's what you have in mind. See this page, for example. — EdM, Nov 28 '22 at 19:36
I am hoping to make sure that pairs have the same general direction, is there a way to visualize that? — user321627, Nov 28 '22 at 20:08
Can you provide more details (and even better, the intervals you want to visualize)? There are two sets of data and also 10 pairs of treatments? How are the confidence intervals estimated? — dipetkov, Dec 03 '22 at 14:11

score 2 · Accepted Answer · answered Dec 02 '22 at 19:50

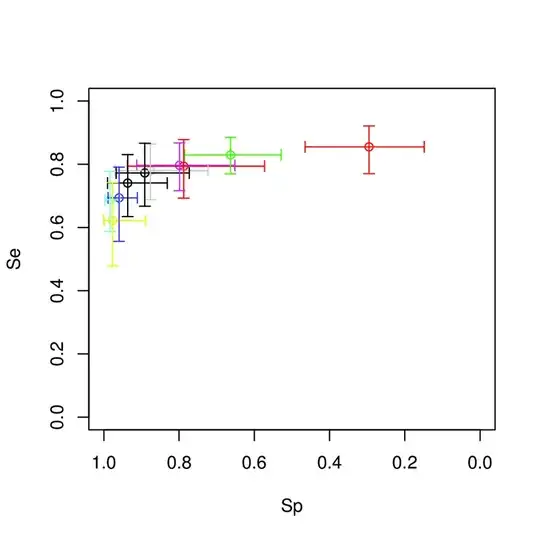
I have pairs of intervals, where each pair has an interval corresponding to treatment and then treatment .

If the intervals corresponding to the two treaments are completely independent, then a cross-hair plot like you show is a simple and reasonable way to display the intervals. The drawback is that they don't represent anything related to the distribution of values or model estimates along each cross-hair, just the values at the pre-specified interval limits.

If you do have more information about the distribution of values or estimates along the intervals, then you might consider shading, color coding, or additional cross-hatch marks along each cross-hair to display that aspect of the data.

Shading or coloring would be particularly useful if the responses to the two treatments were themselves paired within each pair of intervals: for example, if each pair of intervals represents responses by a group of individuals each of whom received both treatments. Then you would have correlated estimates of the joint responses to the treatments within each pair of intervals, which could be displayed in a set of 2D contour or density plots.

What is an effective way to visually compare many sets of confidence intervals?

1 Answers1