What you’ve described can’t happen in math, so there’s either a missing detail, a bug in your code causing you to input something other than what you intend to input, or something wrong with the Python function (the last of which I find unlikely).
I disagree with this Python implementation of $R^2$, but for the same data set, $R^2_{1,sklearn}>R^2_{2,sklearn}\iff MSE_2>MSE_2\iff R^2_{1,Dave}>R^2_{2,Dave}$. This is because $R^2$, either in the implementation you use or that way I prefer, is a strictly decreasing function of MSE.
$$R^2=1-\dfrac{MSE}{denominator}$$
(This denominator is some kind of sum of squares that is related to a model that predicts the same value every time. Your function and I disagree on what the one value should be, but you could pick $5$ or $17$ or $\pi$ as the denominator, and MSE and that definition of $R^2$ should move in opposite directions.)
If you evaluate the $R^2$ of two different models but on the same data, the denominator stays the same. Thus, increasing/decreasing $R^2$ corresponds to decreasing/increasing MSE.
(If your implementation of an MSE calculation involves an $n-p$ denominator instead of $n$ or $n-1$, then the above does not apply. This could be the kind of missing detail I mentioned in the last sentence of my first paragraph.)
MAE is a totally different metric that need not increase/decrease with an increase/decrease in MSE or a decrease/increase in $R^2$. In this linked answer of mine, I give examples where an MSE increase/decrease is accompanied by an MAE decrease/increase.
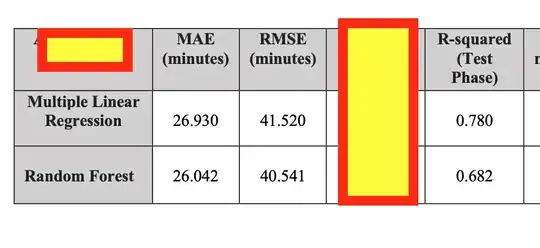
r2_score? – Richard Hardy Oct 15 '22 at 18:03