4

If I fit a regular linear mixed model to my data with lmer, I get a pattern of residuals that, at a glance, looks to me to deviate from Gaussian in two ways. The residuals are obviously very heavy-tailed, and there are a lot of discussions on Cross Validated of how to address heavy-tailed distributions. But, for example, a commonly used distribution to address heavy tails, the Student's t distribution, doesn't capture this histogram at all. The residuals are both heavy tailed and pointy -- there are extreme outliers and a lot of tight clustering around the mean. Is there a distribution I can use as a link function in a generalized linear model (or some other approach) that would capture the actual shape of these residuals?

Here's a density plot for the dependent variable:

enter image description here

Here's one for the residuals in a linear mixed model:

enter image description here

Here's the Q-Q plot for the residuals:

enter image description here

EDIT:

Here's a residual versus fitted plot, to show the heteroskedasticity:

enter image description here

ANOTHER EDIT:

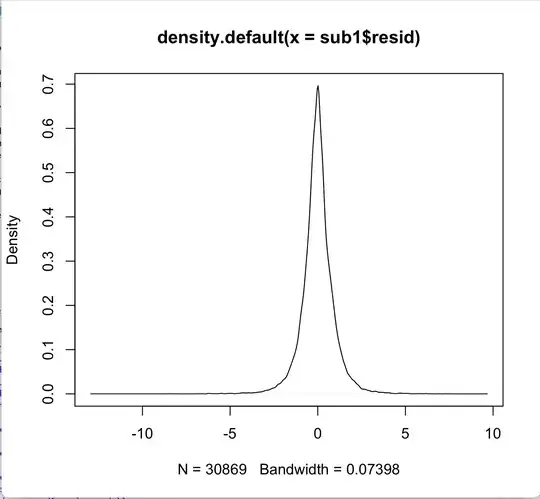
Here are density plots of subsets of the residuals, split at fitted = 1.1, in an effort to show the two distributions of the residuals with roughly homogeneous variance:

enter image description here

enter image description here

Katie
  • 263
  • 1
    The first thing that comes to mind is the double exponential distribution. It looks like there's a nimble package that might help (rdocumentation.org/packages/nimble/). – gung - Reinstate Monica Sep 29 '22 at 15:39
  • I'm pretty sure you couldn't use that with the generalized linear model, though. For estimation (fitting the model), a linear model would probably work. For testing, you'd want to use something other than the p-values that come by default. Eg, bootstrapping might work. – gung - Reinstate Monica Sep 29 '22 at 15:47
  • Thanks! I felt like I had seen a distribution that looked like mine before and I think that was it. It looks like maybe I could also use brms to model data with a double exponentional: https://www.rdocumentation.org/packages/brms/versions/1.3.1/topics/set_prior – Katie Sep 29 '22 at 16:21
  • we could try implementing the Generalized Gaussian in glmmTMB ... https://en.wikipedia.org/wiki/Generalized_normal_distribution – Ben Bolker Sep 29 '22 at 19:18
  • Oops, generalized normal won't work in glmmTMB because the log-likelihood is non-differentiable with respect to mu. I wonder how brms handles it ... ??? – Ben Bolker Sep 29 '22 at 20:10
  • https://en.wikipedia.org/wiki/Kurtosis#The_Pearson_type_VII_family ???? – Ben Bolker Sep 29 '22 at 20:13
  • Presumably you need a generalized linear mixed model? If you just want a log-linear model with a conditional distribution like this (no random effects), then it's a whole lot easier ... Can you clarify? – Ben Bolker Sep 29 '22 at 21:16
  • Yes, I have a mixed model with nested random effects. In fact, I have two random effects that are crossed and nested within a third. We were discussing my model here (https://stackoverflow.com/questions/73855415/how-to-specify-a-model-with-more-than-one-nested-random-effect-in-heavy-packag) before I realized that student's t didn't capture the true shape of my distribution at all. – Katie Sep 29 '22 at 21:26
  • Do you have a summary of your data & experiment design? – dipetkov Sep 30 '22 at 14:56
  • @dipetkov is this helpful? https://docs.google.com/document/d/1BeM9k6jxYpHWp9ElSkQnB0J5nUxbctqsQ-JfZkeAToA/edit?usp=sharing – Katie Sep 30 '22 at 15:32
  • Thanks. I admit I don't understand this... So I'm not sure whether/how you can implement this but if I were you, I would consider simplifying the model instead of making it more complex with fancy distributions, by analyzing summaries (instead of the "raw" data). In the simplest case, the summaries are averages (perhaps average over clusters? any grouping of measurements where the fixed effects of interest do not vary might be a good candidate for the analysis of summaries approach). – dipetkov Sep 30 '22 at 15:55
  • Hi @dipetkov if I can be clearer in any specific way, please let me know. I already average over a single cluster, and I have also tried averaging over all clusters (which doesn't really change the the distribution of the data). It is also eliminates a variable to compute the relevance contrasts. I would be very happy to have a simpler model with fewer fixed effects, but from experience in various experiments with lmer and rlmer all the fixed effects are important. There are complicated interactions in this experiment (which shouldn't really surprise me theoretically). – Katie Sep 30 '22 at 16:16
  • @Katie any chance to share a ( sample,) of your data ? Asking to see if a simple Lambert W x Gaussian Transform + OLS could help you here. – Georg M. Goerg Oct 26 '23 at 03:31

3 Answers3

5

  1. You can't interpret the shape of the residuals without checking the conditional mean and variance assumptions (e.g. by residuals vs fitted); if the model for the conditional mean was wrong or the residuals were heteroskedastic, you could see a residual pattern like that even though the errors were normal.

  2. Assuming that's all fine, there's not a GLM that will do it, but an L1 regression (least absolute deviations regression) model might work reasonably well for conditional distributions close to a Laplace (you might want to check that the logs of the bin counts decrease roughly linearly either side of the mode; it can sometimes be hard to judge directly from the histogram, but it looks reasonable).

    For an identity link and constant variance function, L1 regression is easy to do in R with quantreg::rq (with tau at the default value). There's other possible packages, but that's the one I'd look at first.

Glen_b
  • 282,281

  • I'll edit with a residuals vs. fitted plot. The distribution is in fact somewhat heteroskedastic, particularly on the right side.

  • I had started looking at quantreg, and then lqmm, yesterday in response to I don't know what I read. Can quantreg be used for mixed models? The vignette doesn't make that clear. lqmm apparently can although I was struggling to figure out how to specify my model; but that seems a more appropriate question for Stack Overflow.

    • – Katie Sep 30 '22 at 12:55
  • Yeah, that will tend to make the marginal distribution look peaker and heavier tailed than the conditional distribution (what assumptions relate to) would look. I was concerned that your tails might even be a bit heavier than Laplace but now with the look of that heteroskedasticity, perhaps the conditionals will be somewhat less heavy tailed than it. You seem to have a lot of data so you might consider slicing into a few more or less homogenous sections and looking at distributions of residuals with those. $,$ ... ctd
    • – Glen_b Oct 01 '22 at 01:44
  • . . . I'd at least consider seeing the effect of a split at about fitted=1.1 there, so having two separate residual histograms. $,$ 2. I believe lqmm would be mixed models. I don't think quantreq includes mixed models but I've only ever used rq in it, so I could have missed something. – Glen_b Oct 01 '22 at 01:47
  • I just made density plots for the split distribution and added them to the post. The higher variance ones actually seem better behaved. – Katie Oct 02 '22 at 19:21
  • Thanks. TBH, looking at the heavier tailed one, I'd be inclined to use least absolute deviations still for the whole thing. – Glen_b Oct 03 '22 at 06:19